Caribou !

Statistiques et Modélisation

Il est toujours assez étonnant de voir à quel point le statisticien n’est pas perçu à sa juste valeur par l’individu lambda de notre société… Qui n’a jamais entendu le fameux « ouarf les statistiques, on sait jamais d’où elles sortent ni comment ou par qui elles sont faites, il y a surement une arnaque quelque part ! ». Mais pardonnons-leur leur incultisme à ce sujet !

Cette passionnante discipline qu’est celle des Statistiques (et de la Modélisation, mot qu’on oublie trop souvent de lui associer) est en plein essor du fait du pouvoir de décision qu’elle détient au cœur d’un projet nécessitant une évaluation complète du risque pour passer d’une phase de développement à une autre. Ainsi cette discipline, en quantifiant l’information de manière rigoureuse et théoriquement solide, a permis le passage du choix binaire (oui/non) au choix flexible argumenté par la connaissance de la probabilité d’échec induite (nous pourrons désormais choisir « oui » si le risque associé est faible et « non » si ce dernier est trop important). Nous comprenons aisément pourquoi l’individu qui sait manier les Statistiques est alors celui détenant toutes les clés pour l’aboutissement d’un projet, en devenant même l’un des chaînons secrets, véritable éminence grise, les plus importants. Mais la discipline ne se résume pas qu’à cela, notons aussi ses qualités indéniables et incontestables dans la construction de plans d’expérience et de sondage robustes assurant la fiabilité des résultats à venir sur des sous-échantillons représentatifs d’un contexte ou encore ses liens permanents avec des disciplines primordiales comme la théorie de la mesure, l’algèbre linéaire, l’analyse numérique, les séries de Fourier ou encore les algorithmes de la bio-informatique poussant toujours un peu plus l’élaboration théorique et l’apparition de nouvelles méthodologies. Les Statistiques sont ainsi l’opportunité de découvrir un nombre extrêmement varié de domaines d’application tel que la biologie, l’écologie, l’agroalimentaire, le marketing, le sport, la santé, l’industrie etc. ; car si d’entières différences sont flagrantes entre ces contextes multiples, le statisticien aura toujours la capacité de rajouter sa pierre à l’édifice du fait d’outils d’analyse adaptables à n’importe lequel d’entre eux.
Enfin, cette discipline ne serait pas ce qu’elle est sans le folklore qui l’entoure ! Sa capacité à modéliser un phénomène et donc ses qualités prédictives ne peuvent qu’ajouter à son caractère séducteur, ainsi le statisticien n’est plus uniquement celui qui donne une photographie de ce qu’il observe mais il devient en quelque sorte un être surnaturel capable de prédire le futur, rien que cela ! Alors finalement ? Qui peut oser en dire autant !?

L’objectif de ce site est de rassembler, de la manière la plus exhaustive qui soit, l’ensemble des techniques de production et redressement des données, des tests statistiques, outils d’analyse exploratoire et méthodes d’analyse supervisée et non supervisée existantes. Il est également question de présenter la théorie se cachant derrière chaque outil en présentant les algorithmes associés tout en indiquant les syntaxes sous R et SAS pour les mettre en œuvre. J’ai fait en sorte qu’il soit utile aussi bien au jeune diplômé qui recherche des informations pratiques et théoriques pour combler sa culture statheuse (oui, le ‘h’ est mis exprès par référence au mot « math » , il s’agit pour moi de la marque différenciant le simple statisticien utilisateur d’histogrammes sans savoir comment ça marche de celui capable de maîtriser la théorie et ainsi être plus performant dans l’usage des méthodes de Statistiques et Modélisation) qu’à la personne non affiliée à la discipline et qui se sent perdue lorsqu’elle se trouve face à son jeu de données et son désir compulsif de le faire parler.
L’Autre raison de la création de ce site est également dû aux multiples collaborations récentes que j’ai eu avec des étudiants en thèse venant de tous horizons ainsi que d’une réelle volonté de partager ma passion. Il est donc viser de créer un espace d’échanges dans le but d’élargir cette communication, proposant ainsi mon expertise sur d’autres projets (aussi n’hésitez pas à me contacter même si je suis souvent over-pris de par mes fonctions professionnelles !!!).

Le site a vu le jour en 2013, au travers de multiples fiches déposées et pour la plupart assez sommaire. Depuis 2020, j’ai commencé à passer chacune d’elle en version 2, visant à être plus homogène, intégrant systématiquement une partie exemple et les codes sous R et SAS. Ce travail devrait être bouclé pour le second semestre 2024 et restera encore insuffisant. Dès la fin de l’année, les fiches passeront petit à petit en version 3, bouclant le travail d’homogénéisation amorcé, il est prévu de : mieux expliquer chaque outil, compléter certaines parties encore trop sommaire, rajouter les codes C, JAVA, SPSS, Python et, soyons fou, Excel-macro. Une fois ce travail réalisé, un nouveau des plus ambitieux débutera, en 2026-2027, visant à mettre toutes ces fiches sous LaTeX et proposer une encyclopédie gratuite en ligne et téléchargeable. J’espère pour cette étape trouver un confrère, tout aussi passionné, qui pourra m’assister dans les parties les plus théoriques qui me font défauts.

Avant de conclure cette page de présentation, je tiens également à souligner le fait qu’il s’agit d’un site fait par passion pour ce domaine qu’est la Statistique, la Probabilité et la Modélisation et principalement motivé par les trois faits suivants : parfaire mes propres connaissances, centraliser les informations essentielles de chaque outil et offrir à l’intéressé le détail et l’application de ces différents outils (combien de fois ai-je trouvé de jolies formules théoriques ne servant à rien, « coucou les documents sur l’analyse discriminante de Fisher » pour ne citer qu’eux). Toutefois, comme tout site présent sur internet, il n’est pas exempt de tout reproche et ceci en dépit des efforts de rigueur effectués, de nombreuses coquilles sont encore beaucoup trop présentes. Il sera donc toujours vivement conseillé de croiser les informations que vous pourrez en extraire avec d’autres sources afin de les valider (notamment celles indiquées dans la partie bibliographique des différents articles) et je dirais même : bien fou est celui qui se basera sur mon site pour en tirer des vérités absolues. Il est question ici de proposer un espace décrivant les différents outils de statistique et modélisation avec mes mots à moi et ma propre interprétation, rien de plus.

Enfin, car un bon site est un site capable de s’auto-hors-sujet avec panache! Sévissant sur cette formidable île tourmentée qu’est devenue Mayotte en tant qu’ingénieur ayant pour ambition de contribuer à son développement, c’est avec émotion que j’alimente ce site en promouvant le dernier, et de loin le plus féerique, département français (bon OK, à égalité avec la Corse…).

Ce site est dédié à cette petite femme de gauche au cœur immense et cet ours polaire fada de l’OM, deux personnes exceptionnelles, qui me servent de parents.

Enfin je souhaite rendre hommage, dans un premier temps, aux trois personnes suivantes : Gilbert Saporta, Stéphane Tufféry et Ricco Rakotomalala, véritables sources d’inspiration lors de mes études et début de ma carrière professionnelle. Ne les connaissant pas personnellement, je continue de caresser délicatement le doux rêve de les rencontrer un jour (je m’imagine déjà complètement hystérique et perdu dans l’érection intellectuelle ce jour-là, je les plains d’avance et espère qu’ils sauront me pardonner).

Et dans un second temps, à tous ces célèbres mathématiciens (R. A. Fisher, K. Pearson, J. Neyman, A. Wald, G. E. P. Box, B. Efron, L. Breiman, J. Tukey, A. N. Kolmogorov, H. Hotelling, W. G. Cochran, C. R. Rao, D. Cox, etc.) à qui nous devons notre discipline et qui ont réussi l’exploit de faire de l’or avec de l’oxygène. C’est grâce à leur travaux que notre civilisation ne cesse d’évoluer dans le bon sens (lorsque c’est le cas…) et rares sont ceux qui sont suffisamment intéressés et informés pour s’en rendre compte. Au nom de notre espèce, il convient de les remercier et de leur rendre hommage chaque jour pour leurs découvertes et ce qu’elles nous ont apporté et continuent de nous apporter quotidiennement : Merci.

Les modèles épidémiologiques

De gauche à droite : Daniel Bernoulli, Ronald Ross, William Ogilvy Kermack, Anderson Gray McKendrik et Richard Doll

Historique :

Sommaire :

• Présentation
• Les modèles épidémiologiques
  • Du modèle au modèle
  • Le compartiment et le modèle
  • Le modèle métapopulationnel
  • Les effets naissances, migrations et décès naturels
  • Quelques autres compartiments classiques
  • Le nombre de reproduction effectif
• Annexe théorique
  • Les Equations Différentielles Ordinaires
  • L’Algorithme d’Euler
  • L’Algorithme de Runge-Kutta
• Exemple
  • Le modèle
  • Le modèle métapopulationnel
• Application sous R
• Application sous SAS
• Bibliographie

Présentation :

Les modèles compartimentaux épidémiologiques sont une famille d’outils d’anticipation et de compréhension des dynamiques de propagation des maladies, jouant un rôle central dans le domaine de la Santé publique. Ils ont fait énormément parler d’eux au cours de la crise Covid-19 mondiale traversée de 2020 à 2022. Leur principe consiste à s’appuyer sur une liste de paramétrages contextuels pour ensuite proposer une série de projections sur un nombre fixé de temps.

Les modèles épidémiologiques ont évolué au fil du temps grâce aux contributions de nombreux chercheurs, mathématiciens et épidémiologistes. Néanmoins, certaines figures clés ont marqué des étapes cruciales dans leur développement. On pourra citer Daniel Bernoulli qui, au XVIIIème siècle, a jeté les bases de la modélisation des phénomènes aléatoires, élément clé des modèles épidémiologiques. Bases qui ont été ensuite développées par Ronald Ross en contribuant à la modélisation mathématique des maladies infectieuses, notamment le paludisme, éclairant la compréhension de sa transmission par les vecteurs. Parmi les autres célébrités à évoquer, et cet article pêchera dans l’exhaustivité de cette liste, on peut également parler de William Ogilvy Kermack et d’Anderson Gray McKendrick qui, en 1927, publient un article fondateur introduisant le modèle précurseur des modèles épidémiologiques complexes modernes. Enfin, deux dernières personnalités emblématiques : Richard Doll et Austin Bradford Hill, qui ont joué un rôle important dans la formalisation des études épidémiologiques et notamment établi les principes cruciaux sur la causalité entre des facteurs spécifiques et des maladies.

Ces outils se basent sur la notion de système d’Equations Différentiels Ordinaires (EDO) et de leur résolution afin de déterminer à chaque itération les différents volumes associés aux compartiments considérés, permettant alors à tracer la courbe d’évolution de l’épidémie selon autant d’angles qu’il y a de compartiments.

Les modèles épidémiologiques :

Hypothèse préliminaire : Un jeu de paramètres en adéquation avec les différents compartiments utilisés.

– Du modèle au modèle

Il faut définir au préalable une unité de temps : , et son maximum : . De cette manière, on fixe déjà la temporalité  sur laquelle la modélisation sera réalisée. Enfin, on note la somme des effectifs de tous les compartiments utilisés, soit la population total étudiée.

Il y a deux compartiments classiques dans les modèles épidémiologiques : le pour « Susceptibles », soit les susceptibles d’être contaminés car sains, et il ne faut pas confondre un individu sain avec un individu immunisé. Le pour « Infectés », soit les individus sains qui ont fini par être contaminés. On fixe alors le paramètre , probabilité qu’un individu fasse la transition : à chaque instant . Ces deux premiers compartiments forment à eux-seuls le modèle , regroupant de façon simpliste l’ensemble des infections virales chroniques n’ayant aucune incidence sur la mortalité (on pourra citer par exemple l’herpès simplex dont on ne meurt et ne guérit pas). On peut exprimer les volumes/effectifs à l’instant au sein de chacun de ces deux compartiments sous la forme généralisée :

, à ce stade les paramètres sont supposés nuls, on y reviendra plus tard. On définit alors les états initiaux : , et on érige le système sous la forme du système d’Equations Différentielles à résoudre suivant :

A noter que l’un des indicateurs phares utilisés pour le suivi des épidémies est celui du nombre ou incidence de nouveaux cas. On peut l’obtenir alors très facilement en l’extrayant de la formule, et de forme :

On enrichit le modèle en introduisant maintenant la notion de guérison grâce au compartiment . Dès lors, on passe du phénomène assez rare d’infections virales chroniques sans réelle conséquence à n’importe quelles maladies dont on guérit mais ne meurt pas, spectre particulièrement large et dont on pourrait citer le rhume en guise d’exemple. L’ajout de ce compartiment se fait avec celui du paramètre traduisant mathématiquement le taux de guérison. Le volume/effectif associé au compartiment à l’instant est alors :

A noter que l’insertion de ce nouveau compartiment a également une incidence sur le compartiment comme on peut le voir sur l’intégrale généralisée décrite précédemment. On définit alors les états initiaux : , et on érige le système sous la forme du système d’Equations Différentielles à résoudre suivant :

Enfin, on rajoute maintenant un dernier compartiment relatif aux décès : . Il s’agit des personnes infectées par la maladie et qui en sont décédées. Ces modèles permettent ainsi d’intégrer toute maladie à risque endémique avec un potentiel risque de mortalité. Sa mise en place s’accompagne de l’ajout du paramètre retranscrivant le taux de mortalité. Le volume/effectif associé à ce compartiment et à l’instant est alors :

Tout comme pour le compartiment , l’insertion du compartiment a également une incidence sur le compartiment comme on peut le voir sur l’intégrale généralisée décrite précédemment. On définit alors les états initiaux : , et on érige le système sous la forme du système d’Equations Différentielles à résoudre suivant :

– Le compartiment et le modèle

Le principal défaut que l’on peut trouver au modèle , outre sa simplicité, est de ne pas prendre en compte le principe d’incubation d’une maladie. Il s’agit plus particulièrement du temps écoulé entre la contamination et le début des symptômes, soit, d’une certaine manière, la longueur de la flèche : . Ce qui vaut à ce principe un compartiment à part entière et noté : , c’est qu’en plus de créer un décalage dans le temps de la propagation du virus étudié, il permet de prendre en compte le stade de progression de la maladie chez un individu infecté qui, méconnaissant son statut réel pourra en contaminer d’autres qui sont sains et sans s’en rendre compte. Dès lors, le terme d’Exposés est utilisé. Cet enrichissement permet aux modèles épidémiologiques de s’approcher toujours un peu plus des mécanismes des maladies à risque endémique et modifie sensiblement la forme généralisée du volume/effectif associée au compartiment du fait de liaison imbriquée :

, en définissant le nouveau paramètre

On fixe les états initiaux : , et on érige le système sous la forme du système d’Equations Différentielles à résoudre suivant :

– Le modèle métapopulationnel

Une manière d’améliorer le modèle construit est d’intégrer dans son schéma d’Equations Différentielles l’information sur le taux de contact entre les différentes classes d’âge d’une population. Par exemple, si l’on suppose que l’épidémie que l’on cherche à modéliser se déroule dans un pays avec un moyenne d’âge particulièrement jeune, ajouter un paramètre qui permettra de pondérer le taux de transmission en fonction du taux de contact inter-classe d’âge pourra apporter un boost de précision très intéressant.

On doit donc définir ce l’on appelle une matrice de contacts de forme symétrique suivante :

, avec les différentes classes ou intervalles d’âge paramétrés et le taux de contact entre les classes d’âge et . Le modèle épidémiologique s’en voit fortement enrichi puisqu’il intègre dans son concept les probabilités de transiter d’une classe d’âge à l’autre. Si l’on prend par exemple le modèle , on intègre ce concept ainsi :

, avec et des vecteurs de taille des volumes ventilés par classe d’âge.

– Les effets naissances, migrations et décès naturels

Les modèles vus précédemment sont plus souvent utilisés pour les épidémies ponctuelles et sont d’ailleurs assez flexibles pour procéder à des réajustements lors d’une propagation en cours ou même établir des scénarios servant à modéliser plusieurs vagues successives. Pour cela il suffit simplement d’adapter les paramètres initiaux à la situation rencontrée. A partir du moment où l’objectif devient la modélisation d’un phénomène s’allongeant dans le temps, il est important d’intégrer dans son modèle les notions de :

• Nouvelles naissances, qui implique que la population croît régulièrement sur un profil bien spécifique venant ainsi alimenter uniquement le compartiment . Cet effet sera noté ;
• Effets migratoires, avec une perte ou un gain de population. Les notions de cas importés et autochtones prennent tout leur sens, et de fait, venant alimenter tous les compartiments. Cet effet sera noté ;
• Décès naturels, à ne pas confondre avec les décès du compartiment directement liés à la maladie modélisée, et donc de diminution de la population, touchant alors tous les compartiments également. Cet effet sera noté .

Si l’on souhaite enrichir à nouveau le modèle vu précédemment, cela donne, pour les états initiaux :

– Quelques autres compartiments classiques

Enfin, il est possible de rajouter pléthore de compartiments différents et variés dans l’objectif de coller au mieux au contexte : 

• Le compartiment des vaccinés, noté , intégrant à la fois le taux de vaccinés de départ et celui de nouveaux vaccinés ;
• Le compartiment des mis en quarantaine, noté , intégrant le taux de mis en quarantaine, de guéris et de décès en quarantaine ;
• Le compartiment des asymptomatiques, noté , intégrant le taux d’infectieux asymptomatiques qui présentent un enjeu important lors du contrôle d’une épidémie du fait qu’ils sont capables d’infecter d’autres porteurs sains et quasi-impossible à repérer ;
• Le compartiment des immunisés après infection et guérison, noté , et son taux associé ;
• Le second compartiment qui permet de remettre en jeu les individus infectés, guéris et non immunisés dans le premier compartiment , et son taux associé.

– Le nombre de reproduction de base

Le ou « Nombre de Reproduction de Base » est une mesure cruciale en épidémiologie, offrant des indications sur la transmission d’une maladie dans une population (à ne pas confondre avec le volume/effectif d’individus du compartiment , des guéris, à l’instant initial ). Il s’agit du nombre moyen d’infections secondaires résultant d’un individu infecté introduit dans une population totalement susceptible. Autrement dit, il mesure la capacité d’une maladie à se propager à travers une population. Son calcul est dépendant du type de modèle utilisé. En reprenant les notations précédentes, en voici plusieurs de ses formes :

– Pour le modèle , ;

– Pour le modèle , ;

– Pour les modèles , et , ;

– Pour le modèle , ;

– Pour le modèle , .

Il est également possible de déterminer le nombre moyen de nouvelles infections à un instant et noté (nombre de reproduction effectif instantané). Sa formule, quel que soit la forme du modèle est :

La différence essentielle entre et est en fait liée à son objectif d’utilisation. Par exemple, pour qualifier une maladie spécifique, le apportera une information sur sa vitesse de propagation globale permettant de caractériser son niveau de dangerosité. Alors que le trouve son intérêt dans le suivi d’une épidémie en tant qu’indicateur synthétisant son stade d’évolution, souvent utilisé en Santé publique afin déterminer la dimension des mesures de contrôle à mettre en œuvre.

En termes de lecture, un correspond à une épidémie en pleine propagation puisqu’un individu infecté en contamine au moins un, lorsqu’elle stagne avec un infecté qui contamine un seul sain, et pour son déclin, un infecté en contamine moins d’un.

A noter que les formules du et du reposent sur des hypothèses simplificatrices, telles que l’homogénéité de la population et la constance des paramètres. Dans des contextes plus complexes, où ces conditions ne sont pas remplies, des ajustements et des modèles plus élaborés peuvent être nécessaires pour les évaluer.

Annexe théorique :

– Les équations différentielles ordinaires

Les modèles épidémiologiques à compartiments se basent sur la notion de système d’Equations Différentielles Ordinaires (EDO). Pour obtenir une prévision à un instant , on résout ce système donnant les différents volumes associés aux différents compartiments. Une EDO à l’ordre est de la forme générale : 

, avec fonction adaptée à la forme des compartiments que l’on veut considérer dans le modèle et de forme : 

Les EDO disposent de plusieurs propriétés essentielles et offrant aux modèles épidémiologiques compartimentaux des caractéristiques des plus pratiques :

– Le théorème d’existence et d’unicité de Picard-Lindelöf et de Cauchy-Lipschitz permet aux EDO, sous certaines conditions, d’admettre une solution qui existe et est unique, relativement aux conditions initiales données ;

Théorème : Soit une équation différentielle ordinaire du premier ordre avec la condition initiale , où est continue dans une région rectangulaire et . Si est Lipschitz continue par rapport à dans , c’est-à-dire qu’il existe une constante telle que pour tous et dans , alors l’EDO a une unique solution dans un intervalle , où est le plus petit des nombres et .

– De ce théorème découle également le concept d’EDO autonome, assurant son indépendance en fonction du temps. Cela signifie que les taux de variation des variables dépendent uniquement des valeurs actuelles des variables, et non du temps ;

– Le critère de stabilité de Nyquist et le critère de Hurwitz assure la stabilité linéaire pour les systèmes dynamiques décrits par des EDO. Pour les solutions non linéaires, c’est le théorème de stabilité de Lyapunov qui joue un rôle fondamentale. La notion de stabilité indique comment les solutions réagissent aux petites perturbations des conditions initiales ;

Définition : Soit un système dynamique décrit par l’équation différentielle alors le critère de stabilité de Nyquist s’applique à un système linéaire sous la forme de fonction de transfert déterminé par,

1. avec variable de Laplace.
2. Elle admet des valeurs spécifiques de sur le plan complexe le long de l’axe imaginaire , unité imaginaire et fréquence angulaire.
3. Après tracé de la fonction , on peut conclure en la stabilité du système si et seulement si la courbe ne contourne pas le point critique .

Définition : Soit un système dynamique décrit par l’équation différentielle alors le critère de stabilité de Hurwitz s’applique à un système polynomial déterminé par,

1. L’équation : .
2. On détermine la matrice de Hurwitz associée aux coefficients de cette équation.
3. On peut conclure en la stabilité du système si et seulement tous les mineurs principaux, ou déterminants associés aux sous-matrices, sont strictement positifs.

Définition : Soit un domaine contenant l’équilibre d’un système dynamique décrit par l’équation différentielle : , où est un vecteur d’état dans est une fonction continue, et est un point d’équilibre tel que .

Supposons qu’il existe une fonction continue définie positive, c’est-à-dire que , avec . De plus, considérons une fonction définie sur telle que sa dérivée le long des trajectoires du système soit semi-définie négative, c’est-à-dire .

Alors, l’équilibre est stable au sein de Lyapunov. Si, de plus, , alors l’équilibre est asymptotiquement stable au sens de Lyapunov. En d’autres termes, la fonction est une fonction Lyapunov candidate, et la dérivée joue le rôle d’une mesure de la stabilité du système. Si est toujours négative (ou nulle), cela indique que le système est stable ou asymptotiquement stable, respectivement, autour de l’équilibre .

Ces caractéristiques des EDO font qu’elles sont couramment utilisées pour modéliser les systèmes dynamiques. Ces systèmes peuvent représenter divers phénomènes, tels que la croissance de la population, les mouvements planétaires, les réactions chimiques, etc. On peut les résoudre selon deux principales méthodes : l’algorithme de Newton et l’algorithme de Runge-Kutta.

– L’Algorithme d’Euler

L’algorithme d’Euler est une méthode itérative numérique, proposée par Leonhard Euler au XVIIIème siècle, utilisée pour résoudre des équations différentielles ordinaires. Dans le contexte des modèles épidémiologiques, cette méthode peut être appliquée pour résoudre des systèmes d’équations différentielles non linéaires, généralement associés à des modèles plus complexes. C’est une méthode itérative qui se base sur le principe que, près d’une solution, une fonction peut être approximée par une droite tangente à la courbe. Les itérations successives conduisent à une convergence rapide vers la solution.

Étapes de l’algorithme,

1. Initialisation : Définir une équation différentielle , un pas de temps et une condition initiale ;
2. Itérations :
   • ;
   • Avec , une estimation de , et est la dérivée de par rapport à évaluée en .
3. Répéter l’étape deux jusqu’à atteindre la fin de l’intervalle temporel spécifié.

– L’Algorithme de Runge-Kutta

L’algorithme de Runge-Kutta, développé par les mathématiciens allemands Carl Runge et Martin Kutta au début du XXe siècle, constitue une avancée significative dans la résolution numérique d’EDO. Leur objectif était d’améliorer la méthode d’Euler, en proposant une approche plus précise et stable pour approximer les solutions d’EDO. Les méthodes numériques Runge-Kutta, notamment celle d’ordre () sont aujourd’hui les plus largement utilisées pour résoudre une variété de problèmes scientifiques, y compris les modèles mathématiques en épidémiologie, en offrant un bon compromis entre précision et complexité. Cet algorithme utilise des coefficients pour pondérer les pentes de la fonction à différents points le long du pas de temps. L’itération est répétée jusqu’à ce que la solution soit calculée sur tout l’intervalle temporel souhaité.

Étapes de l’algorithme,

1. Initialisation : Définir une équation différentielle , un pas de temps et une condition initiale ;
2. Itération :
   • Calculer les coefficients intermédiaires , et comme suit,
     • ;
       
     • ;
     • ;
     • .
   • Mettre à jour la solution ;
   • Mettre à jour le temps : ;
3. Répéter l’étape deux jusqu’à atteindre la fin de l’intervalle temporel spécifié.

Exemple :

Le modèle

On cherche à modéliser la propagation d’une maladie sur un territoire selon un modèle qui correspond parfaitement aux attentes puisque l’on dispose des paramètres associés. Ainsi, on définit le taux de contamination , avec une durée d’incubation de « temps » le taux d’incubation , le taux de guérison et le taux de décès associé à , . On veut que ce modèle donne des prévisions sur « temps » avec un pas .

Enfin, on initialise la modélisation avec individus sains, infecté introduit dans la population concernée et dont les symptômes ne sont pas encore apparus (« exposé »), infecté avec symptômes, guéri et décédé par la pathologie . Soit un effectif total . 

Ainsi, pour ,

, avec à ce temps, un nombre de nouveaux cas de :

Pour ,

, avec à ce temps, un nombre de nouveaux cas de :

Pour ,

, avec à ce temps, un nombre de nouveaux cas de :

On continue les calculs jusqu’à avoir parcouru tous les temps . Et si l’on affiche le graphe que l’on obtient avec les différents vecteurs associés à chacun des compartiments alors on obtient la figure suivante :

A la fin de cette vague, on extrait les indicateurs de Santé publique associés à l’épidémie de la maladie suite à son introduction au sein de la population que l’on observe :

– individus ont été infectés, soit  de la population totale ;

– individus en sont décédés, soit de la population totale ;

– Le pic de l’épidémie a eu lieu à avec nouveaux cas à ce temps-là.

Le modèle métapopulationnel

On cherche à modéliser la propagation d’une maladie sur un territoire selon un modèle qui correspond parfaitement aux attentes puisque l’on dispose des paramètres associés. Ainsi, on définit le taux de contamination , avec une durée d’incubation de « temps » le taux d’incubation , le taux de guérison et le taux de décès associé à , . On veut que ce modèle donne des prévisions sur « temps » avec un pas .

On inclut également la matrice de contacts entre les différentes classes d’âge que l’on a à disposition. Ces classes d’âge sont construites selon un découpage en cinq intervalles de même longueur :

Enfin, on initialise la modélisation avec individus sains pour les différentes classes d’âge, infecté, de 0-20 ans, introduit dans la population concernée et dont les symptômes ne sont pas encore apparus (« exposé »), infecté avec symptômes, guéri et décédé par la pathologie .

Soit un effectif total,

Ainsi, pour ,

, avec à ce temps, un nombre de nouveaux cas par classe d’âge de :

Pour ,

, avec à ce temps, un nombre de nouveaux cas par classe d’âge de :

Pour ,

, avec à ce temps, un nombre de nouveaux cas par classe d’âge de :

On continue les calculs jusqu’à avoir parcouru tous les temps . Et si l’on affiche le graphe que l’on obtient avec les différents vecteurs associés à chacun des compartiments  et sommés sur les effectifs ventilés par classe d’âge à chaque instant , alors on obtient la figure suivante :

A la fin de cette vague, on extrait les indicateurs de Santé publique associés à l’épidémie de la maladie suite à son introduction au sein de la population que l’on observe :

– individus ont été infectés, soit  de la population totale ;

– individus en sont décédés, soit de la population totale ;

– Le pic de l’épidémie a eu lieu à avec nouveaux cas à ce temps-là.

[latex]\bullet[/latex] Application sous R :

On proposera la fonction suivante permettant de produire des modélisations incluant les compartiments  :

Model_epidemiologique = function(S0,E0,I0,R0,D0,beta,sigma,gamma,delta,pas,T) {

# La fonction s’adapte en fonction du paramétrage rentré. S0 correspond au volume d’individus susceptibles/sains de départ associé à beta le taux de contamination (si <= 0 alors le fonction ne se lance pas), E0 à celui d’exposés/contaminés n’ayant pas encore développé les symptômes associé à sigma le taux d’incubation (si <= 0 alors le compartiment est exclu), I0 à celui d’infectés, R0 à celui des guéris associé à gamma le temps de guérison (si <= 0 alors le compartiment est exclu) et D0 à celui des décédés suite à la pathologie étudiée associé à delta le taux de mortalité lié à la pathologie (si <= 0 alors le compartiment est exclu). Les paramètres pas et T représentant respectivement l’unité de temps et le nombre de temps total parcouru.  

Model_epidemiologique = function(S0,E0,I0,R0,D0,beta,sigma,gamma,delta,pas,T) {

# Si l’on ne veut pas utiliser le compartiment E, et comme l’erreur est facile, on applique un réajustement ici si on s’est trompé
if (sigma == 0 && I0 == 0 && E0 > 0) {
print(« Attention, le paramètre sigma étant nul, le compartiment E ne sera pas utilisé, or sur votre paramétrage Sigma = 0, E > 0 et I = 0, aussi le programme va intervertir les valeurs de E et I »)
I0 = E0
E0 = 0
}

# Chargement de la bibliothèque pour la résolution d’équations différentielles
library(deSolve)

# Fonction générique du modèle SEIRD avec tous les compartiments voulus pour cette fonction
seird_model <- function(t, y, parameters) {
with(as.list(c(y, parameters)), {
dS = (-beta * S * I / N) * pas
if (sigma > 0) {
dE = (beta * S * I / N – sigma * E) * pas
dI = (sigma * E – (gamma + delta) * I) * pas
}
if (sigma == 0) {
dE = 0
dI = (beta * S * I/N – gamma * I) * pas
}
dR = (gamma * I) * pas
dD = (delta * I) * pas
return(list(c(dS, dE, dI, dR, dD)))
})
}

# Conditions initiales
initial_conditions = c(S = S0, E = E0, I = I0, R = R0, D = D0)

# Création du vecteur des différents temps
times = seq(0, T, by = pas)

# Auto-configuration des paramètres du modèle pour l’utilisation de la fonction ode du package deSolve
NAME = « S »
CHOIX = « S »
initiale_state = 1
LEGEND = « Susceptibles »
COL = « blue »
parameters = c(beta = beta)
if (sigma > 0) {
NAME = paste(NAME, « E »)
CHOIX = c(CHOIX, »E »)
LEGEND = c(LEGEND, « Exposés »)
COL = c(COL, « yellow »)
parameters = c(parameters, sigma = sigma)
}
if (beta > 0) {
NAME = paste(NAME, « I »)
CHOIX = c(CHOIX, »I »)
LEGEND = c(LEGEND, « Infectés »)
COL = c(COL, « red »)
}
if (gamma > 0) {
NAME = paste(NAME, « R »)
CHOIX = c(CHOIX, »R »)
LEGEND = c(LEGEND, « Guéris »)
COL = c(COL, « green »)
parameters = c(parameters, gamma = gamma)
}
if (delta > 0) {
NAME = paste(NAME, « D »)
CHOIX = c(CHOIX, »D »)
LEGEND = c(LEGEND, « Décès »)
COL = c(COL, « purple »)
parameters = c(parameters, delta = delta)
}

# Calcul de la population totale pour application des équations différentielles
N = S0 + E0 + I0 + R0 + D0
parameters = c(parameters, pas = pas, N = N)

# Si le paramètre beta est différent de 0 alors on peut lancer la modélisation, si ce dernier est égal à 0, au regard de la formule des équations différentielles, assez logiquement on ne peut lancer les calculs
if (beta > 0) {
# Résolution des équations différentielles avec la fonction ode
result = ode(y = initial_conditions, times = times, func = seird_model, parms = parameters)
# Sélection des colonnes d’intérêt en fonction du type de modèle décrit par les paramètres entrés
result = result[,c(« time »,CHOIX)]

# Tracé des résultats
plot(times, result[, « S »], type = « l », lty = 1, col = « blue », xlab = « Jours », ylab = « Population », main = NAME, ylim = c(0,N))
for (p in 3:dim(result)[2]) {lines(times, result[, CHOIX[p-1]], lty = 1, col = COL[p – 1])}
legend(« topright », legend = LEGEND, col = COL, lty = 1)
}

if (beta == 0) {print(« A minima, le paramètre Beta doit être > 0 »)}
}

On souhaite lancer la modélisation d’un . Pour cela on procède de la manière suivante :

Model_epidemiologique(S0=9999,E0=1,I0=0,R0=0,D0=0,beta=0.05,sigma=0.2,gamma=0.01,delta=0.001,pas=1,T=1000)

Parmi les éléments à insérer les plus importants il faut relever :

–  Le volume de susceptibles de départ : ;

–  Le volume d’exposés de départ : ;

–  Le volume d’infectés de départ : ;

–  Le volume de guéris de départ : ;

–  Le volume de décédés de départ : ;

–  Le taux de contamination : ;

–  Le taux d’incubation : ;

–  Le taux de guérison : ;

–  Le taux de décès : .

On obtient alors les résultats suivants :

, qui sont alors les mêmes que ceux obtenus lors des calculs manuels (cf partie « Exemple »).

Application sous SAS :

On proposera la macro suivante permettant de produire des modélisations incluant les compartiments  :

%macro Model_epidemiologique(S0=, E0=, I0=, R0=, D0=, beta=, sigma=, gamma=, delta=, pas=, T=);

/* La fonction s’adapte en fonction du paramétrage rentré. S0 correspond au volume d’individus susceptibles/sains de départ associé à beta le taux de contamination (si <= 0 alors le fonction ne se lance pas), E0 à celui d’exposés/contaminés n’ayant pas encore développé les symptômes associé à sigma le taux d’incubation (si <= 0 alors le compartiment est exclu), I0 à celui d’infectés, R0 à celui des guéris associé à gamma le temps de guérison (si <= 0 alors le compartiment est exclu) et D0 à celui des décédés suite à la pathologie étudiée associé à delta le taux de mortalité lié à la pathologie (si <= 0 alors le compartiment est exclu). Les paramètres pas et T représentant respectivement l’unité de temps et le nombre de temps total parcouru. */

options nonotes;

%if &beta. > 0 %then %do;

/* Si l’on ne veut pas utiliser le compartiment E, et comme l’erreur est facile, on applique un réajustement ici si on s’est trompé */

%if (&sigma. = 0 and &I0. = 0 and &E0. > 0) %then %do;

%put Attention, le paramètre sigma étant nul, le compartiment E ne sera pas utilisé, or sur votre paramétrage Sigma = 0, E > 0 et I = 0, aussi le programme va intervertir les valeurs de E et I;

%let I0 = &E0.;

%let E0 = 0;

%end;

/* Initialisation des compartiements */

%let N = %sysevalf(&S0. + &E0. + &I0. + &R0. + &D0.);

%let S = &S0.;

%let E = &E0.;

%let I = &I0.;

%let R = &R0.;

%let D = &D0.;

data Modelisation;

t = 0;

S = &S0.; E = &E0.; I = &I0.; R = &R0.; D = &D0.;

dS = 0; dE = 0; dI = 0; dR = 0; dD = 0;

N = &N.;

run;

/* Algorithme de calcul des différents compartiments à chaque instant t */

%do t = 1 %to &T.;

%put &t.;

/* Compartiment Susceptibles */

%let dS = %sysevalf(-(&beta. * &S. * &I. / &N.) * &pas.);

/* Compartiment Exposés & Infectés */

%if &sigma. > 0 %then %do;

%let dE = %sysevalf((&beta. * &S. * &I. / &N. – &sigma. * &E.) * &pas.);

%let dI = %sysevalf((&sigma. * &E. – (&gamma. + &delta.) * &I.) * &pas.);

%end;

/* Version du compartiment Infectés si celui Exposés n’est pas enclenché */

%if &sigma. = 0 %then %do;

%let dE = 0;

%let dI = %sysevalf((&beta. * &S. * &I./&N. – &gamma. * &I.) * &pas.);

%end;

/* Compartiment Guéris */

%let dR = %sysevalf((&gamma. * &I.) * &pas.);

/* Compartiment Décès */

%let dD = %sysevalf((&delta. * &I.) * &pas.);

/* Mise à jour des compartiements */

%let S = %sysevalf(&S. + &dS.);

%let E = %sysevalf(&E. + &dE.);

%let I = %sysevalf(&I. + &dI.);

%let R = %sysevalf(&R. + &dR.);

%let D = %sysevalf(&D. + &dD.);

data ajout;

t = &t.;

S = &S.; E = &E.; I = &I.; R = &R.; D = &D.;

dS = &dS.; dE = &dE.; dI = &dI.; dR = &dR.; dD = &dD.;

N = S + E + I + R + D;

run;

data Modelisation;

set Modelisation ajout;

run;

%end;

/* Tracé des résultats */

proc sgplot data=Modelisation;

series x = t y = S / legendlabel = « Susceptibles » lineattrs = (color = blue);

%if &sigma. > 0 %then %do;

series x = t y = E / legendlabel = « Exposés » lineattrs = (color = yellow);

%end;

series x = t y = I / legendlabel = « Infectés » lineattrs = (color = red);

%if &gamma. > 0 %then %do;

series x = t y = R / legendlabel = « Rétablis » lineattrs = (color = green);

%end;

%if &delta. > 0 %then %do;

series x = t y = D / legendlabel = « Décès » lineattrs = (color = purple);

%end;

xaxis label = « Temps »;

yaxis label = « Population »;

keylegend / location = inside position = topright;

run;

%end;

%if &beta. = 0 %then %do;

%put Beta doit être supérieur à 0;

%end;

options notes;

%mend;

On souhaite lancer la modélisation d’un . Pour cela on procède de la manière suivante :

%Model_epidemiologique(S0=9999, E0=1, I0=0, R0=0, D0=0, beta=0.05, sigma=0.2, gamma=0.01, delta=0.001, pas=1, T=100);

Parmi les éléments à insérer les plus importants il faut relever :

–  Le volume de susceptibles de départ : ;

–  Le volume d’exposés de départ : ;

–  Le volume d’infectés de départ : ;

–  Le volume de guéris de départ : ;

–  Le volume de décédés de départ : ;

–  Le taux de contamination : ;

–  Le taux d’incubation : ;

–  Le taux de guérison : ;

–  Le taux de décès : .

On obtient alors les résultats suivants :

, qui sont alors les mêmes que ceux obtenus lors des calculs manuels (cf partie « Exemple »).

Bibliographie :

– A contribution to the mathematical theory of epidemics de W. O. Kermack et A. G. McKendrick ; 

– Infectious diseases of humans : Dynamics and control de R. M. Anderson et R. M. May ;

–  On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations de O. Diekmann, J. A. Heesterbeek et J. A. Metz ;

– The mathematics of infectious diseases de H. W. Hethcote ; 

–  Modeling infectious diseases in humans and animals de M. J. .Keeling et P. Rohani ;

– Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission de P. Van den Driessche et J.  Watmough ; 

– Appropriate models for the management of infectious diseasesde H. J. Wearing, P. Rohani et M. J. Keeling ; 

– Le site web : https://images.math.cnrs.fr/Modelisation-d-une-epidemie-partie-1.html ;

– Simulation des Equations Différentielles Stochastiques sous R de A. C. Guidoum.

 

Les réseaux de neurones

Warren McCulloch (à gauche) et Walter Pitts (à droite)

Historique :

Sommaire :

• Présentation
• Les réseaux de neurones
  • Vocabulaire
  • L’algorithme
  • Autres particularités
  • Les réseaux à base radiale
• Annexe théorique
• Exemple
• Application sous R
• Application sous SAS
• Bibliographie

Présentation :

Les réseaux de neurones ou neuronale, outil d’analyse supervisée qui prend ses racines dans les années 1940 et connait un essor constant de développement depuis, permet de discriminer une matrice de variables réponses de n’importe quel format (continue, binaire, etc.) à partir d’une matrice de variables explicatives, également de n’importe quel format, .

Les réseaux de neurones se sont construits une solide réputation au fil du temps, marquée par des hauts et des bas, dépendante de l’engouement mais aussi de la lassitude du moment. Relégués au statut de boîte noire, ils demeurent aussi riches que leur histoire. Initialement conceptualisés par Warren McCulloch et Walter Pitts en 1943, introduisant la notion de neurone formel, leur idée était de s’inspirer des neurones et des synapses du cerveau humain et de les mathématiser. Le concept a progressé, et en 1950, cette idée a pris forme avec la création du Perceptron par Frank Rosenblatt. Malheureusement, en 1969, Marvin Lee Minsky et Seymour Papert ont souligné d’importantes limites théoriques, entraînant une chute vertigineuse de l’enthousiasme généré, jusqu’au début des années 1980.

En 1982, John Joseph Hopfield introduit une version portant son propre nom et généralise la notion de base des neurones connectés de McCulloch et Pitts. Puis, en 1986, David Rumelhart, Geoffrey Hinton et Ronald J. Williams développent l’algorithme de rétropropagation du gradient pour l’apprentissage, faisant tomber un à un les détracteurs des réseaux de neurones. Cela ressuscite tout l’engouement qu’ils avaient généré autrefois et les propulse jusqu’à une utilisation courante en industrie à partir des années 1990. Leur essor reprend ainsi de plus belle et, dans les années 2000 avec l’augmentation exponentielle de la puissance de calcul des ordinateurs, valide l’arrivée des réseaux de neurones profonds (DNN), convolutionnels (CNN) et récurrents (RNN). Les désagréments théoriques balayés, les réseaux de neurones peuvent s’épanouir, permettant des avancées significatives dans le domaine du traitement du langage naturel. Depuis les années 2010, ils accumulent de nombreux succès remarquables dans divers domaines tels que le traitement de l’image, la traduction automatisée et la santé.

Malgré les éloges envers les réseaux de neurones, il faut rappeler qu’il s’agit d’un outil d’une haute complexité, manquant de lisibilité, capable de reproduire n’importe quelle fonction, notamment en raison de leur paramétrage et du risque accru de sur-apprentissage du phénomène que l’on cherche à modéliser ou encore de la convergence vers une solution globale et non locale. D’une certaine manière, ils sont déjà limités à une utilisation sur de grandes bases de données pour justement minimiser ce risque.

Enfin, bien que présentés ici comme un outil de classification et de prédiction, il existe également une version pour mener des analyses non supervisées, comme les cartes auto-organisatrices de Kohonen.

Les réseaux de neurones :

Hypothèse préliminaire : Tout format de variable et .

Vocabulaire

Avant de se lancer dans une vision plus approfondie des réseaux de neurones, il est important de rappeler le vocabulaire associé.

– Neurones, ou nœuds, et connexions synaptiques : unités de traitement, ou calculateur, interconnectées par des poids synaptiques. Chaque connexion synaptique a un poids qui détermine l’importance de la contribution d’un neurone à l’activation d’un autre ;

– Architecture ou topologie : structure du réseau distinguée généralement selon trois types. La couche d’entrée qui recevra les données initiales, les couches cachées qui effectueront les transformations intermédiaires, la couche de sortie qui retournera la modélisation finale. Dès lors où l’on aura plusieurs couches cachées on parlera de réseaux de neurones profonds ;

– Fonction d’activation ou de transfert : introduit la non-linéarité dans le réseau et ainsi la capacité de cet outil à modéliser des relations complexes. Cette dernière interviendra lors de la propagation avant alors que sa dérivée interviendra lors de la rétropropagation ;

– Propagation avant (feedforward) : les données circulent à travers le réseau de la couche d’entrée à la couche de sortie sans rétroaction. Chaque neurone transmet son activation aux neurones de la couche suivante. Il s’agit de la partie non supervisée de l’algorithme car ne faisant pas intervenir la réponse ;

– Rétropropagation (backpropagation) : ajustement des poids synaptiques du réseau en fonction de l’erreur calculée entre la sortie prédite et la sortie réelle. Son objectif est de minimiser cette erreur en temps réel, en ajustant les poids de manière itérative. il s’agit de la partie supervisée de l’algorithme ;

– Fonction de coût : mesure de l’écart entre la sortie prédite et la sortie réelle que la rétropropagation va chercher à chaque itération de minimiser ;

– Taux d’apprentissage : servant à déterminer la taille du pas que l’algorithme de rétropropagation prend pour ajuster les poids du réseau. Plus il est haut et plus la convergence est rapide au risque de s’arrêter sur une solution locale et non globale. Alors que plus il est faible, plus l’on devra utiliser d’itérations pour obtenir la convergence, favorisant ainsi les chances de trouver la solution globale.

Enfin, afin d’avoir une vision simple de toutes ces notions, on conclura avec la graphique suivant :

L’algorithme

On part d’une matrice , avec  variables explicatives et variables à prédire.

L’algorithme que l’on proposera n’intègre que les concepts de rétropropagation et d’apprentissage profond. Il s’approche plus particulièrement d’un type de réseau de neurones qui porte le nom de Perceptron multicouche. En voici les différentes étapes :

Etape 1 : Choix du paramétrage du réseau de neurones,

• On définit le nombre de couches cachées. Pour chaque couche , on désigne un nombre de neurones . On a volontairement mis la paramétrage possible à couche cachée afin de rappeler qu’il est possible, revenant à faire une simple régression linéaire ou logistique en fonction de la fonction d’activation choisie. Plus l’on ajoute de couches cachées et plus le pouvoir prédictif du modèle s’en voit amélioré, mais c’est aussi là que réside l’un des plus gros risques de surapprentissage. De nombreux auteurs proposent des méthodes différentes pour le choix du nombre de couches cachées. S. Tufféry, par exemple, indique qu’il faut compter à individus pour ajuster chaque poids et qu’il vaut mieux se concentrer sur l’utilisation au maximum de deux couches cachées puis jouer sur les autres paramètres pour améliorer son réseau de neurones. 
• On définit la fonction d’activation. La plus communément utilisée est la fonction logistique ou sigmoïde et de dérivée : . Mais on en retrouve d’autres qui le sont également dans une moindre mesure,

– ReLU (Rectified Linear Unit) : , appréciée par sa simplicité et sa capacité à résourdre le problème du gradient pour certaines types de réseau. Sa dérivée est si et si ;

– Leaky ReLU (Unité Linéaire Paramétrique) : , variation de ReLU permettant l’utilisation d’un « petit » gradient lorsque l’entrée est négative. Sa dérivée est si et si . On peut également parler de la version Parametric ReLU (PreLU) avec qui n’est plus fixé comme un paramètre mais va bénéficier du processus d’apprentissage de l’algorithme pour s’optimiser ;

– Tangente hyperbolique : , similaire à la fonction sigmoïde mais bornée sur , utile pour certains types de réseau nécessitant que les données soient normalisées. Sa dérivée est ;

– ELU (Unité Linéaire Exponentielle) : si , si , introduisant le concept de saturation pour les valeurs négatives du fait de la convergence vers de l’exponentielle dans ces cas-là. Sa dérivée est si , si ;

– Softmax : , à privilégier dans le cadre où est composée d’une ou plusieurs variable(s) multiclasse(s), il convient alors en amont d’en produire le tableau disjonctif complet. D’ailleurs, la remarque s’applique également si c’est le cas de . Sa dérivée est si et si ;

– Swish : , avec la fonction sigmoïde, permettant d’améliorer les performances dans certains cas de l’utilisation de la fonction ReLU. Sa dérivée est .

Le choix de la fonction d’activation se fait en lien avec la nécessité d’avoir une fonction linéaire au voisinage de et non linéaire aux extrémités. Enfin, la standardisation ou la normalisation des données est souvent conseillée en privilégiant des variables variant dans ou afin de contrôler le calcul des poids, favorisant alors certaines variables au détriment de la qualité prédictive du modèle final.

• On définit les poids (synaptiques) initiaux associés aux différentes couches. De préférence, aléatoirement. En effet, démarrer avec des poids identiques risque fortement d’entrainer la non-différenciation des neurones. Ce phénomène est connu sous le terme de « problème des neurones morts », diminuant leur capacité d’apprentissage. Xavier Glorot propose de délimiter le périmètre de tirage en divisant chacun des poids par : . Pour chacune des couches cachées , on notera la matrice des poids de taille si , si . Enfin, il faut également attribuer à la couche de sortie ses propres pondérations , tirées de la même manière et de taille . A noter que l’ajout de systématiquement est lié au besoin d’avoir, sans que cela soit obligatoire mais simplement conseillé, une ligne supplémentaire de poids associés aux termes constants.
• On définit le taux d’apprentissage , qui servira à fixer la vitesse de correction des matrices de pondérations. Ce dernier étant un pourcentage, il doit être compris dans ;
• On définit un nombre d’itérations à appliquer afin d’arrêter l’algorithme qu’il converge ou non.

Etape 2 : Propagation avant (apprentissage non supervisé), en notant le produit matricielle, on applique l’algorithme suivant,

• Pour la première couche cachée : ;
• Dès la seconde couche cachée : ;
• Pour la couche de sortie :

En fait, cette étape de l’algorithme remet un peu en question la vision traditionnelle du réseau de neurones que l’on veut à tout prix opposer à celle du cerveau, ce qui est normal puisqu’il s’agit du concept de base à l’origine de l’outil. Mais on comprend mieux certaines présentations qui consistent à le représenter comme une succession de « plaques » contre lesquels l’on va jeter notre jeu de données, l’éparpillant matriciellement pour à nouveau le rejeter comme une nouvelle plaque qui va l’éparpiller à son tour. Et ainsi de suite jusqu’à ce qu’à force d’exploser nos données, elles finissent par se remettre dans le bon ordre. On retrouve ici l’approche non supervisée puisque l’on n’utilise pas notre réponse dans la propagation.

Enfin, à noter que cette partie de l’algorithme fait également aussi office de règle décisionnelle. Munis des poids et d’un nouvel individu décrit selon les caractéristiques utilisées pour le paramétrage, il suffit d’appliquer les itérations indiquées précédemment pour obtenir sa prédiction.

Etape 3 : Calcul de l’erreur, on compare la sortie prédite avec la réponse en utilisant une fonction de coût. Cette fonction mesure la différence entre la prédiction du réseau et les classes réelles. On a l’embarras du choix à nouveau :

– L’erreur quadratique moyenne (MSE) : , le classique du genre. On peut précéder à sa variante consistant à appliquer le facteur au lieu de ou encore celle s’affranchissant de l’élévation au carré pour les valeurs absolues (MAE), moins sensible aux valeurs aberrantes que la MSE. Elles sont alors réservée à une ou plusieurs réponse(s) continue(s) ;

– L’entropie croisée binaire (Binary Cross-Entropy) : , réservée à une réponse univariée binaire et donc souvent associée à la fonction d’activation sigmoïde ;

– L’entropie croisée catégorielle (Categorical Cross-Entropy) : , réservée à une réponse univariée à plusieurs classes et donc souvent associée à la fonction d’activation softmax.

Etape 4 : Rétropropagation (apprentissage supervisé), l’erreur calculée est propagée en sens inverse à travers le réseau. Les poids synaptiques sont ajustés de manière itérative pour minimiser cette erreur. Cela se fait en utilisant la descente de gradient, où la dérivée partielle de la fonction de coût. en notant le produit terme à terme,

– On démarre sur la couche de sortie,

• Initialiser , sachant que certains réseaux programmés font intervenir la dérivée de la fonction coût à la place de la formule proposée ;
• Calculer les corrections des poids de la couche de sortie

– Puis sur la dernière couche cachée,

• Mettre à jour la dérivation , la matrice des poids de la couche de sortie est utilisée cette fois-ci en lui retirant la première ligne ;
• Calculer les corrections des poids de la dernière couche cachée en faisant intervenir la dérivée de la fonction d’activation , et en notant le produit terme à terme, 

– Puis en poursuivant couche par couche en sens inverse, ,

• Itérativement mettre à jour la dérivation , la matrice des poids de la couche est utilisée en lui ôtant la première ligne ;
• Calculer les corrections des poids de la couche ,

– Enfin, une fois arrivé à la première couche,

• On met à jour la dérivation , la matrice des poids de la seconde couche est utilisée en lui supprimant la première ligne ;
• Calculer les corrections des poids de la première couche,

Etape 5 : On dispose désormais des matrices de correction des différentes couches . Et on applique ces corrections en une seule fois : 

L’algorithme de la descente du gradient, présenté ici, est le plus répandu mais demeure cependant sensible aux minimums locaux. Parmi les autres méthodes existantes : l’algorithme de Levenberg-Marquardt optimal pour les petits réseaux, quasi-Newton, gradient conjugué meilleur compromis pour les réseaux complexes, propagation rapide ou encore les algorithmes génétiques. Concernant celui présenté ici, on peut retrouver dans la littérature plusieurs amélioration comme l’optimisation stochastique, la régularisation (pour éviter le surapprentissage) et des techniques avancées telles que les algorithmes Adam, RMSprop, etc.

– Etape 6 : Sur le nombre d’itérations défini en guise de paramétrage, on répète les étapes à jusqu’à ce que le modèle atteigne une performance satisfaisante sur les données d’entraînement.

Enfin, et comme tout bon outil de type data mining, il convient de valider le modèle construit par précédés empiriques. On lance alors ces étapes sur un échantillon d’apprentissage obtenu soit en scindant l’échantillon de base (cross-validation, LOOCV, tirage aléatoire de deux tiers de l’échantillon) et de valider la modèle « tuné » obtenu sur un échantillon test. L’objectif étant d’obtenir les mêmes performances sur échantillon test et échantillon de validation. Si c’est le cas on peut le valider, sinon il faut en reconstruire un nouveau.

Autres particularités

Comme indiqué, l’algorithme présenté ici est assez incomplet vis à vis de ceux des véritables réseaux de neurones implémentés sur bon nombre de langage de programmation de nos jours. Parmi les nombreux concepts non évoqués précédemment on a :

– La convolution, donnant leur nom aux réseaux CNN, consiste à appliquer un filtre (ou noyau) directement sur . Son but est de détecter les motifs spatiaux dans les données d’entrée. Si l’on avait voulu intégrer ce concept dans l’algorithme présenté ci-dessus, grosso-modo il aurait fallu définir de deux nouveaux jeux de pondérations dédiés (filtres), appliquer la convolution des données d’origine avec le premier filtre translaté par le second. Cela définit l’étape en amont, ensuite on applique les étapes suivantes pour la propagation. Pour la rétropropagation, l’application de la convolution se fait cette fois-ci à la toute fin de l’algorithme, via processus inversé.

– La normalisation par lots (Batch Normalization) est un concept introduit pour résoudre les problèmes de convergence « lente », d’explosions du gradients et ainsi gagner en stabilité du modèle. Initialement développé pour les CNN, elle est désormais utilisée pour tout type de réseau. Il s’agit de composer un certain nombres de sous-échantillon des données d’origine, appelés mini-batch, et pour chaque sortie de neurone , on va appliquer la Batch Normalisation au travers de la formule suivante :

, avec paramètre d’échelle, paramètre de translation et constante ajoutée pour évitée la division par . A noter qu’il y a autant de paramétrages que de couches cachées considérées dans la structure du réseau.

Concrètement et si l’on reprenait l’algorithme décrit, cela reviendrait à appliquer la fonction d’activation après Batch Normalisation du produit scalaire pour la propagation. Et lors de la rétropropagation, appliquer le processus de calcul inversé sur et à chaque couche. Une fois de plus, le paramètre , taux d’apprentissage, servira à fixer à quelle vitesse on rectifie les paramètres et .

Un mot sur le réseau résiduel (Residual Networks ou ResNets) dont le concept vise à introduire des sauts de connexion pour faciliter le flux d’information à travers le réseau, permettant l’entrainement de réseaux beaucoup plus profonds. Souvent couplé à la Batch Normalisation, il s’agit alors de l’appliquer sur certaines couches et pas systématiquement à toutes.

– Et encore de nombreux et autres nombreux concepts, tels que les fonctions d’erreur ou coût adaptatives, les méthodes de régularisation (régression Ridge, Lasso, Elasticnet, etc.), les méthodes des moments permettant de contrôler le risque que les pondérations partent dans un unique sens et aillent s’enterrer vers une solution locale, etc., que l’on ne définira pas ici. L’on invitera alors le lecteur à se fournir en ouvrage spécialisé sur le sujet tant il y en a pléthore.

Les réseaux à base radiale :

On dénombre énormément de type de réseaux différents, adaptés selon le format des données en entrée comme par exemple celles appariées ou temporelles. Une fois de plus, il est conseillé de s’orienter ensuite vers des ouvrages spécialisés. Toutefois, on pourra laisser un mot sur l’une des alternatives les plus connues au Perceptron Multicouche, les réseaux à base radiale (RBF).

Ils se distinguent par une architecture composée d’une couche d’entrée, d’une unique couche cachée utilisant des fonctions radiales comme la fonction gaussienne avec distance euclidienne entre le point d’entrée et le centre et le paramètre de largeur gaussienne ou écart-type, et d’une couche de sortie. La notion de centre dans un RBF consiste à en définir un pour chaque neurone de la couche cachée, soit un point dans l’espace d’entrée du réseau. 

Les RBF présentent les avantages d’une capacité à apprendre à modéliser des relations non linéaires grâce aux fonctions radiales et sont moins sensibles au surajustement par rapport au Perceptron Multicouche. Quant aux inconvénients majeurs, ils nécessitent la sélection des centres et des paramètres radiaux parfois difficile ainsi que des performances potentiellement inférieures sur des tâches plus complexes comparées aux Perceptron Multicouche.

Annexe théorique :

On présentera ici une esquisse de la démonstration de l’apport de l’algorithme de rétropropagation sur la qualité de modélisation des réseaux de neurones.
En notant le taux d’apprentissage, poids de la couche cachée , l’algorithme de la descente de gradient lors de l’étape de rétropropagation s’exprime ainsi :

L’apport de la rétropropagation sur l’estimation des paramètres provient du terme qui est l’erreur de prédiction et servira à ajuster et réajuster les matrices des poids de chaque couche. En notant la fonction coût qui mesure l’écart entre valeurs prédites et valeurs réelles, On peut plus précisément écrire :

, avec,

– mesure comment le coût varie par rapport à la sortie de la couche de sortie. Cela donne une indication de la sensibilité de la fonction de coût aux changements dans la prédiction ;

– représente la dérivée de la fonction d’activation par rapport à son entrée. Cette dérivée mesure comment de petits changements dans l’entrée de la couche de sortie affectent la sortie elle-même.

Maintenant, pour le taux d’apprentissage , on applique la fonction coût à la formule d’actualisation des poids, et selon le développement de Taylor on a :

Si est faible, alors la mise à jour des poids est stable, tandis que si elle est importante, la mise à jour devient significative. Dès lors, le taux d’apprentissage va permettre un équilinre entre converge rapide et stabilité à l’entraînement.

Exemple :

Soit l’échantillon suivant,

Ci-dessous le nuage de point basé sur ces données,

En vert la classe « A » et en rouge la classe « B »

On cherche donc à déterminer une fonction permettant de prédire les deux classes de en fonction des valeurs de . Comme il s’agit d’un exemple, on s’affranchira de la construction par apprentissage statistique. De plus, on ne procèdera pas à la standardisation des variables en amont.

On opte pour le paramétrage suivant :

– Une architecture formée d’une couche d’entrée à neurones (en lien avec le nombre de variables explicatives). couches cachées, l’une à neurones et la seconde à neurones, et une couche de sortie à un neurone (en lien avec le nombre de variable à prédire et son nombre de classes) ;

– La fonction d’activation choisie sera la fonction sigmoïde : , de dérivée ;

– La fonction coût : ;

– Le taux d’apprentissage : ;

– Et pour les poids, on tire aléatoirement ceux associés à la première couche cachée de taille , nombre de neurones de la couche d’entrée, soit deux car deux variables explicatives et nombre de neurones paramétrée sur cette couche cachée :

, à la seconde couche cachée de taille (nombre de neurones de la première couche cachée puis de la seconde couche) :

, et à la couche de sortie de taille (nombre de neurones de la seconde et dernière couche et nombre de réponse de , ici une seule) : 

L’étape d’initialisation étant réglée, on passe à la suite avec l’utilisation de l’algorithme de propagation avant. Donc, pour l’itération N° ,

– La phase de propagation, en débutant par celle dans la première couche se calcul via :

On obtient alors,

– Pour celle de la seconde couche :

– Et enfin, la couche de sortie :

Avant de passer à l’étape de rétropropagation, on calcul le taux d’erreur global, en créant un vecteur numérique associé à la réponse , le fixant à pour la classe « A » et à pour la classe « B ». Selon la fonction coût retenue :

– La phase de rétropropagation. Avant, on va calculer et incrémenter le terme : 

, et maintenant la matrice correctrice des poids associées à la couche de sortie :

Avant de procéder à la rétropropagation sur la seconde couche cachée, on met à jour :

Et puis on travaille sur la seconde couche, en faisant intervenir la dérivée de la fonction d’activation, d’où l’utilisation du terme :

Avant de boucler la rétropropagation, on met à nouveau à jour :

Et enfin, on travaille sur la première couche cachée, en faisant à nouveau intervenir la dérivée de la fonction d’activation :

Les termes d’ajustement sont désormais tous déterminés, il ne reste plus qu’à les appliquer :

–

–

–

Les trois jeux de pondérations étant désormais mis à jour, on peut lancer la seconde itération. Sans reprendre les calculs, car il s’agit exactement des mêmes et seul vont changer, on obtiendra pour itérations, la courbe de l’évolution de l’erreur de prédiction suivante :

Au bout de itérations, l’algorithme converge. On a ainsi les pondérations finales suivantes :

Les performances obtenues peuvent être décrites au travers de la matrice de confusion suivante :

, soit un taux de bonne classification globale de . Enfin, et plus concrètement, on peut afficher le découpage du plan comparé aux classes réelles.

Les bandes rouges correspondent à la région de la classe « A » construite par le modèle, en bleu celle de la classe « B ». En rouge les données réelles de la classe « A » et en vert celles de la classe « B »

Application sous R :

Soit l’exemple suivant :

BDD = data.frame(Y = c(rep(0,10),rep(1,10)),
X1 = c(8.1472, 9.0579, 1.2699, 9.1338, 6.3236, 0.9754, 2.7850, 5.4688, 9.5751, 9.6489, 1.5761, 9.7059, 9.5717, 4.8538, 8.0028, 1.4189, 4.2176, 9.1574, 7.9221, 9.5949),
X2 = c(3.1101, 4.1008, 4.7876, 7.0677, 6.0858, 4.9309, 4.0449, 3.0101, 5.9496, 6.8729, 1.0898, 1.9868, 2.9853, 10.0080, 8.9052, 8.0411, 2.0826, 1.0536, 9.0649, 10.0826))

Package et fonction R: neuralnet: Training of Neural Networks (r-project.org)

La fonction neuralnet du package du même nom permet de réaliser des réseaux de neurones. Après chargement du package, on lance sa conception de la manière suivante :

neuralnet(Y ~ x1 + x2, data = BDD, hidden = c(3,6), algorithm = « backprop », learningrate = 0.1, act.fct = « logistic », linear.output = FALSE, lifesign = « full », constant = TRUE)

Parmi les éléments à insérer les plus importants il faut relever :

–  La formule définissant variable réponse (à gauche) et variables explicatives (à droite) : ~ ;

–  La base de données sur laquelle on souhaite travailler : ;

– Le nombre de couches cachées et de neurones par couche : ;

– L’utilisation de l’algorithme de rétropropagation : ;

– Le taux d’apprentissage nécessaire pour définir la vitesse à laquelle on rectifie les pondérations : ;

– La fonction d’activation, ici la fonction sigmoïde : ;

– L’affichage de tous les résultats obtenus : ; 

– Le choix d’un modèle non linéraire : .

On obtient alors les résultats suivants :

, avec, à gauche, les poids finaux par couche et, à droite, les scores de prédiction.

Les différences obtenues avec les calculs manuels (cf partie « Exemple ») sont explicables du fait que la fonction neuralnet est bien plus complète et permet de lancer des réseaux de neurones bien plus élaborés que celui présenté dans cet article.

Application sous SAS :

Soit l’exemple suivant :

data BDD;
input x1 x2 Y;
cards;
8.1472 3.1101 0
9.0579 4.1008 0
1.2699 4.7876 0
9.1338 7.0677 0
6.3236 6.0858 0
0.9754 4.9309 0
2.7850 4.0449 0
5.4688 3.0101 0
9.5751 5.9495 0
9.6489 6.8729 0
1.5761 1.0898 1
9.7059 1.9868 1
9.5717 2.9853 1
4.8538 10.0080 1
8.0028 8.9052 1
1.4189 8.0411 1
4.2176 2.0826 1
9.1574 1.0536 1
7.9221 9.0649 1
9.5949 10.0826 1
;
run;

Le logiciel SAS offre un module complet pour la production de réseaux de neurones : SAS Visual Data Mining and Machine Learning. Cependant, ce dernier n’est pas disponible dans le package de base, tout comme le module IML pour les calculs matriciels. Par conséquent, on proposera la macro suivante :

%macro neuralNetwork(DATA =, REPONSE =, W =, LEARN_RATE =, ITERATION =, TYPE =);

/* La macro neuralNetwork est disponible pour concevoir son propre réseau de neurones. Sur cette première version, il n’est pas possible de traiter plusieurs réponses Y à la fois. Concernant l’architecture, elle se déploie automatiquement en fonction des matrices de pondérations insérées dans le paramétrage. Par défaut, le programme n’a été implémenté que pour la fonction sigmoïde, des indications dans le code permettent de voir où porter les modifications pour l’ajout d’autres fonctions d’activation.

Paramètres : La base de données DATA et le nom de la variable à discriminer REPONSE, la liste des matrices/vecteurs de pondération W, le taux d’apprentissage LEARN_RATE, le nombre d’itérations à exécuter ITERATION. Si l’on veut utiliser la macro pour classer un nouvelle individu TYPE = C ou pour tuner ses paramètres TYPE = M.

Le programme n’ayant été testé que pour l’exemple qui suit, il est important de conserver les mêmes noms de variables et structure des données. Des mises à jour seront réalisées dans le temps, ajoutant d’autres fonctionnalités */

/* Paramétrage des fonctions pour n’afficher que les erreurs et les warnings */ 

options nonotes spool;

/* Si on veut classer un nouvelle individu, alors on se débarrasse du paramètre sur les itérations en le fixant à 1 puisqu’il s’agit d’utiliser uniquement que la propagation sur les paramètres entrés */

%if &TYPE. = C %then %do;

%let ITERATION = 1;

%put Classification;

%let Obj = Classification;

%end;

/* On renvoi les paramètres du réseau en fonction des matrices des poids utilisées */

%let nbc = %eval(%sysfunc(countw(&W.)));

%do couche = 1 %to &nbc.;

%if &couche. < &nbc. %then %do;

proc contents data = W&couche. out = biblio noprint;

run;

proc sql noprint;

select count(*) into: nb_neurones from biblio;

quit;

%if &couche. = 1 %then %do;

%let neurones = &nb_neurones.;

%end;

%if &couche. > 1 %then %do;

%let neurones = &neurones. &nb_neurones.;

%end;

%end;

%end;

%put Au regard du paramétrage, le réseau programmé aura &nbc. couches cachées, de nombre de neurones respectifs : &neurones.;

/* Pour chaque itération, on applique les étapes de propagation et rétropropagation */

%do it = 1 %to &ITERATION.;

%if &TYPE. = M %then %do;

%put Modélisation;

%put Itération N° &it. sur &ITERATION.;

%let Obj = Modélisation;

%end;

%put Application de la propagation dans un objectif de &Obj.;

/* On lance la propagation pour chaque couche indirectement paramétrée via les poids insérés */

%do couche = 1 %to &nbc.;

%put Sur couche &couche.;

%let cmu = %eval(&couche. – 1);

/* Constitution de la matrice de gauche pour le produit scalaire (1,X) %*% W */

data I_data;

/* Si première couche alors X est la matrice de données d’origine */

%if &couche. = 1 %then %do;

set &DATA.;

drop &REPONSE.;

%end;

/* Pour les couches suivantes, X est H de la couche moins un */

%if &couche. > 1 %then %do;

set H&cmu.;

%end;

/* On créé le colonne associée à la constante de régression */

Cst = 1;

run;

/* L’ordre étant primordial pour le bon déroulement de l’algorithme, on s’assure que la colonne Cst est bien en première */

proc contents data = I_data out = biblio noprint;

run;

proc sql noprint;

select(name) into: list_var separated by ‘,’ from biblio where name ne « Cst »;

quit;

proc sql noprint;

create table I_dataf as select Cst, &list_var. from I_data;

quit;

/* Application du produit sclaire (1,X) %*% W en prenant les bons X et W en lien avec la couche en cours, on créé alors nos matrices H */

%produit_scalaire(A = I_dataf, B = W&couche., Activation = 1);

data H&couche.;

set ResultF;

run;

%end;

/* Si on cherche juste à classifier, alors l’algorithme s’arrête, dans le cas où l’on veut tuner nos paramètres/modéliser, on applique la rétropropagation */

%if &TYPE. = M %then %do;

/* On calcul l’erreur de prédiction afin de constituer le vecteur que l’on pourrait ploter pour voir sa convergence, mais également l’erreur par simple différence nécessaire aux calculs à venir */

data Erreur;

merge &DATA. H&nbc.;

/* Choix de la fonction erreur et sa dérivée */

Erreur = (col1 – &REPONSE.);

Erreur2 = Erreur**2;

keep Erreur Erreur2;

run;

proc sql noprint;

select sum(Erreur2) into: Erreur from Erreur;

quit;

/* Ajout de la nouvelle Erreur calculée aux autres */

data Courbe_erreur_add;

Erreur = 0.5*&Erreur.;

run;

%if &it. = 1 %then %do;

data Courbe_erreur;

set Courbe_erreur_add;

run;

%end;

%if &it. > 1 %then %do;

data Courbe_erreur;

set Courbe_erreur Courbe_erreur_add;

run;

%end;

%put Application de la rétropropagation pour la Modélisation;

/* Algorithme de rétropropagation */

%do couche = 1 %to &nbc.;

/* On inverse l’incrémentation pour retrouver la logique backward */

%let couche_retro = %eval(-(&couche. – &nbc. – 1));

%let cmu = %eval(&couche_retro. – 1);

%put Sur couche &couche_retro.;

/* On crée la matrice t(1,H), matrice à gauche du produit scalaire */

data I_data;

/* En bout de rétropropagation, H est les données d’origine */

%if &couche_retro. = 1 %then %do;

set &DATA.;

drop &REPONSE.;

%end;

/* Sur les couches en sens inverse, on prend le H calculé lors de la propagation */

%if &couche_retro. > 1 %then %do;

set H&cmu.;

%end;

/* On rajoute la Constante */

Cst = 1;

run;

/* On s’assure que la Constante est bien en première colonne */

proc contents data = I_data out = biblio noprint;

run;

proc sql noprint;

select(name) into: list_var separated by ‘,’ from biblio where name ne « Cst »;

quit;

proc sql noprint;

create table I_dataf as select Cst, &list_var. from I_data;

quit;

proc transpose data = I_dataf out = T_I_dataG;

run;

data T_I_dataG;

set T_I_dataG;

drop _name_;

run;

/* Sur la première couche rétropropagée, à savoir la dernière du réseau, on applique la formule t(1,H) %*% fonction coût ou sa dérivée */

%if &couche_retro. = &nbc. %then %do;

/* Matrice à droite du produit scalaire */

data H;

set Erreur;

keep Erreur;

run;

/* Application du produit scalaire et création de la matrice correctice des poids de la dernière couche */

%produit_scalaire(A = T_I_dataG, B = H, Activation = 0);

data dW&couche_retro.;

set ResultF;

run;

%end;

%let nbc_mu = %eval(&nbc. – 1);

%let nbc_md = %eval(&nbc. – 2);

%if &couche_retro. < &nbc. %then %do;

/* Pour les couches, en sens inverse, suivantes, on créé la matrice à droite */

proc contents data = H&couche_retro. out = biblio noprint;

run;

proc sql noprint;

select(name) into: list_mu separated by ‘ ‘ from biblio;

select count(*) into: nb_mu from biblio;

quit;

data H;

merge H&couche_retro.;

%do vmu = 1 %to &nb_mu.;

/* Application de la dérivée de la fonction d’activation, ici la fonction sigmoïde. Afin d’étendre le programme à d’autres fonctions d’activation, il convient de réaliser les ajouts ici de leur dérivée */

h_%scan(&list_mu.,&vmu.,’ ‘) = %scan(&list_mu.,&vmu.,’ ‘) * (1 – %scan(&list_mu.,&vmu.,’ ‘));

drop %scan(&list_mu.,&vmu.,’ ‘);

%end;

run;

/* On récupére la bonne matrice des poids associés à la couche en cours de traitement */

%let cr_pu = %eval(&couche_retro. + 1);

data T_W;

set W&cr_pu.;

/* A laquelle on supprime la première ligne, que l’on transpose ensuite */

if _n_ ne 1;

run;

proc transpose data = T_W out = T_W;

run;

data T_W;

set T_W;

drop _NAME_;

run;

/* Si on est à l’avant-dernière couche, alors exceptionnellement, on prend l’erreur ou sa dérivée directement */

%if &couche_retro. = &nbc_mu. %then %do;

data Erreur;

set Erreur;

drop Erreur2;

run;

%produit_scalaire(A = Erreur, B = T_W, Activation = 0);

/* Et comme pour les couches qui vont suivre on incrémente la dérivation, on l’enregistre afin de l’ajustement couche par couche */

data dh;

set ResultF;

run;

%end;

/* A partir de l’avant-avant-dernière couche, on peut plus facilement automatiser en prenant la dérivation dh incrémentée et l’appliquer directement */

%if &couche_retro. <= &nbc_md. %then %do;

%produit_scalaire(A = dh, B = T_W, Activation = 0);

data dh;

set ResultF;

run;

%end;

/* Reste un dernier produit scalaire à exécuter et sur les matrices réassemblées à gauche et à droite */

data T_I_dataD;

merge H dh;

%do vmu = 1 %to &nb_mu.;

hh_%scan(&list_mu.,&vmu.,’ ‘) = h_%scan(&list_mu.,&vmu.,’ ‘) * %scan(&list_mu.,&vmu.,’ ‘);

drop h_%scan(&list_mu.,&vmu.,’ ‘) %scan(&list_mu.,&vmu.,’ ‘);

%end;

run;

%produit_scalaire(A = T_I_dataG, B = T_I_dataD, Activation = 0);

/* On obtient alors les autres matrices correctices des poids */

data dW&couche_retro.;

set ResultF;

run;

%end;

%end;

/* On applique les corrections dW à nos poids W et ensuite on peut passer à l’itération suivante avec les nouveaux W mis à jour */

%put Mise à jour des poids;

%do couche = 1 %to &nbc.;

proc contents data = W&couche. out = biblio noprint;

run;

proc sql noprint;

select (name) into: list_w separated by ‘ ‘ from biblio;

select count(*) into: nb_w from biblio;

quit;

proc contents data = dW&couche. out = biblio noprint;

run;

proc sql noprint;

select (name) into: list_dw separated by ‘ ‘ from biblio;

quit;

data W&couche.;

merge W&couche. dW&couche.;

%do w = 1 %to &nb_w.;

%scan(&list_w.,&w.,’ ‘) = %scan(&list_w.,&w.,’ ‘) – &LEARN_RATE.*%scan(&list_dw.,&w.,’ ‘);

drop %scan(&list_dw.,&w.,’ ‘);

%end;

run;

%end;

%end;

%end;

/* Que ce soit pour du tuning/modélisation de paramètres, ou de la classification directement, on renvoie la matrice d’origine avec le résultats de ces prévisions que l’on peut traiter à part */

data Classification;

merge &DATA. H&nbc.;

run;

/* Suppression des différentes tables annexes utilisées et sans intérêt */

proc datasets lib = work nolist;

delete varA varB PA PB prod_scal result_add resultF result I_data biblio I_dataF erreur T_I_dataG T_I_dataD dH H T_w courbe_erreur_add;

%do d = 1 %to &nbc.;

delete H&d. Dw&d.;

%end;

run;

/* Réinitialisation des paramètres de la log */

options notes nospool;

%mend;

, qu’il faudra coupler à la macro suivante permettant de calculer les produits scalaires nécessaires :

%macro produit_scalaire(A=, B=, Activation=);

/* Macro pour réaliser un produit scalaire entre deux matrices/vecteurs de données 

   Paramètres : la matrice de gauche A, la matrice de droite B, et si oui (1) ou non (0) on applique au résultat du produit scalaire la fonction d’activation pour chaque cellule/terme. Sur cette première version, seule la fonction sigmoïde a été codée */

/* Nombre de lignes de la matrice de gauche */ 

proc sql noprint;

select count(*) into: nbA from &A.;

quit;

/* Nombre de colonnes de la matrice de droite */

proc contents data = &B. out = varB noprint;

run;

proc sql noprint;

select count(*) into: varB from varB;

select (name) into: listB separated by ‘ ‘ from varB;

quit;

/* Application du produit scolaire */

%do l = 1 %to &nbA.;

%do c = 1 %to &varB.;

/* On récupère les éléments de la ligne l de la matrice de gauche */

data PA;

set &A.;

if _n_ = &l.;

run;

proc transpose data = PA out = PA;

run;

/* On récupère les éléments de la colonne c de la matrice de droite */

data PB;

set &B.;

rename %scan(&listB.,&c.,’ ‘) = T_%scan(&listB.,&c.,’ ‘);

keep %scan(&listB.,&c.,’ ‘);

run;

/* On les superpose, afin de directement multiplier les deux vecteurs en cours de traitement */

data prod_scal;

merge PA PB;

prod = col1*T_%scan(&listB.,&c.,’ ‘);

run;

/* On somme les produits réalisés un à un */

proc sql noprint;

select sum(prod) into: prod_scal from prod_scal;

quit;

/* Adaptée au réseau de neurone, on propose ici de mettre directement l’application de la fonction d’activation ou non, on peut modifier le paramètre Activation si l’on souhaite rajouter d’autres fonctions */

data Result_add;

%if &Activation. = 1 %then %do;

/* Application de la fonction d’activation */

col&c. = 1/(1 + exp(-&prod_scal.));

%end;

%if &Activation. = 0 %then %do;

col&c. = &prod_scal.;

%end;

run;

/* On reconstitue la première ligne des résultats des différents produits scalaires */

%if &c. = 1 %then %do;

data Result;

set Result_add;

run;

%end;

%if &c. > 1 %then %do;

data Result;

merge Result Result_add;

run;

%end;

%end;

/* On rajoute ensuite les nouvelles lignes des résultats des différents produits scalaires */

%if &l. = 1 %then %do;

data ResultF;

set Result;

run;

%end;

%if &l. > 1 %then %do;

data ResultF;

set ResultF Result;

run;

%end;

%end;

%mend;

On lance le réseau de neurones dans un objectif de déterminer le modèle prédictif. On doit alors produire dans un premier temps les différents poids . Etant donné que l’on veut couches cachées à, respectivement, et neurones,

data w1;
input w1_1 w1_2 w1_3;
cards;
-0.5166363 0.9554752 -0.6368997
0.1703469 -0.8107111 -1.0079267
0.3509102 0.6576622 0.6678786
;
run;

data w2;
input w2_1 w2_2 w2_3 w2_4 w2_5 w2_6;
cards;
1.076244 1.2653173 1.6323954 0.26325727 0.1376167 1.0766192
-1.586651 0.3370436 0.5188823 0.65283448 -0.9157413 -0.6095473
-1.382789 0.7540253 -0.8235877 0.01111528 0.3684991 1.4985495
0.712537 -1.8088945 -1.2941944 -0.44789165 -0.1230735 -0.3934913
;
run;

data w3;
input w;
cards;
-0.1755870
1.2174536
0.8050443
0.4084043
1.3316199
1.2032622
-0.3737364
;
run;

On applique la macro de la manière suivante :

%neuralNetwork(DATA = BDD, REPONSE = Y, W = W1 W2 W3, LEARN_RATE = 0.1, ITERATION = 50, TYPE = M);

Parmi les éléments à insérer, il faut relever :

– Le tableau sur lequel on veut travailler : ;

– Le nom de la réponse à discriminer : ;

– La liste des matrices des poids : ;

– Le taux d’apprentissage, qui servira à définir à quel vitesse l’on applique les matrices correctrices des poids : ;

– Le nombre d’itérations à réaliser : ;

– Le mode d’utilisation de la macro : pour tuner les paramètres, pour classer un nouvel individu.

On obtient alors les résultats suivants parmi les tableaux générés en fin de procédure :

, puis :

, et :

La première série de tableaux présente les pondérations finales : . Le quatrième tableau, le taux d’erreur à chaque itération et le dernier la base de données d’origine à laquelle on a inséré les prédictions finales.

L’algorithme implémenté tel quel est particulièrement long en calcul, aussi il n’a été testé que pour itérations, réalisées en minutes, très fortement dépendant de la taille de la base de données du fait de l’application du produit scalaire.

Bibliographie :

– Probabilité, analyse des données et statistiques de Gilbert Saporta ;

– The Elements of Statsticial Learning de Trevor Hastie, Robert Tibshirani et Jerome Friedman ;

– Data mining et statistique décisionnelle, l’intelligence des données de Stéphane Tufféry ;

– Comprendre le deep learning, une introduction aux réseaux de neurones de Jean-Claude Heudin ;

– Le site web : https://datafuture.fr/post/fabrique-ton-premier-reseau-de-neurones/

La L1 de football

 

En 2002, la ligue de Football Professionnelle décidait de passer la première division française de 18 à 20 clubs, augmentant le nombre de journées de championnat à 38 et renommant son championnat en « Ligue 1 de football » (L1). Avec la possibilité d’obtenir 3 points par victoire et 1 par match nul, c’est théoriquement 114 points qu’il est désormais possible de viser au maximum (soit le scénario extrêmement optimiste de 38 victoires en 38 matchs jouées).

Méthodologie

Les données ont été recueillies au travers de trois sources de données :

• Wikipédia, afin de récupérer les informations globales de la saison 2002/2003 à celle d’aujourd’hui ainsi que les évolutions des classements journée après journée de championnat ;
• fr.whoscored.com, afin de récupérer les informations détaillées des équipes à la fin de chaque saison (disponibles qu’à partir de la saison 2009/2010) ;
• transfermarkt.fr, afin de récupérer les listing complets des meilleurs buteurs et passeurs ainsi que les informations complémentaires de la saison 2002/2003 à celle d’aujourd’hui.

Quatre approches sont proposées. Une première purement descriptives sur les indicateurs globaux moyennés sur les 17 saisons considérées (de 2002/2003 à 2018/2019). Le coefficient de corrélation de Spearman a été utilisé pour étudier le lien entre les indicateurs et le classement. La seconde sur les dynamiques des clubs par saison. Le V de Cramer a été utilisé pour étudier le lien entre le classement (découpé en portions) aux différents moments de la saison. L’estimateur de Kaplan-Meier a servi à construire les modèles de survie. Une troisième sur la construction de profils de performance. L’analyse des correspondances multiples (ACM) a été utilisée après avoir transformé l’intégralité des variables continues en variables catégorielles. Et la dernière sur les facteurs de chance de finir européen à la fin de la saison et les facteurs de risque de finir relégable. Un filtre différentiel a été mené dans un premier temps pour filtrer les variables, basé sur le Chi2 de Pearson (et corrigé selon l’approche de Benjamini-Höchberg). Enfin, la régression logistique a permis de caractériser les facteurs de risque/chance.

Les résultats ont été obtenus avec l’automate d’analyse JEAN développé sous SAS.

Indicateurs globaux

Le tableau ci-dessous présente les statistiques principales moyennées sur les 17 saisons considérées.

On peut constater que le premier du championnat cumule en moyenne 83 points tandis que le troisième est à 69 points. Le 5ème a en moyenne 61 points. Concernant la zone de relégation, le premier non relégable doit assurer 40 points voire 41 (si l’on se réfère aux intervalles) pour éviter la 18ème place.

En termes de dynamique, un club qui veut se retrouver européen la saison suivante (au-delà de la 5ème place inclue) doit être en mesure d’assurer une moyenne d’au moins 2 points par match à domicile et 1,4 points à l’extérieur. concernant les clubs ayant l’ambition de survivre en ligue 1, ils doivent assurer respectivement des moyennes de 1,5 et 0,8 soit une dynamique très proche du premier relégable, marquant le fait que la frontière entre ces deux zones est particulièrement fiable. Ce qui les démarquera est plutôt le pourcentage de possession (50 % versus 47 %) et le taux de dribbles réussis par match (8,65 versus 7,63).

Parmi les facteurs fortement corrélés au classement, on peut ainsi retrouver celui de la possession de balle (), du taux de passes réussies () et le nombre moyen de tirs par match (). L’efficacité offensive ressort également, particulièrement pour les quatre premiers du championnat (ratio supérieur à 37 %, ()), alors que pour les autres classés, la distribution semble plus aléatoire.

Enfin, la zone de tir influe également. Les premiers du championnat ont une plus forte tendance à marquer dans les 18 mètres et plus on descend dans le classement et plus l’on constate que les clubs les moins bien classés favorisent des tentatives de marquer depuis l’extérieur de la surface.

Dynamique des clubs

• Historique classement

On s’intéresse maintenant au classement moyen des différents clubs qui ont participé à la L1 au cours des 17 premières saisons.

Sur ces 40 clubs ayant disputé au moins une saison de ligue 1 depuis la saison 2002/2003, seulement deux clubs ont en moyenne toujours étaient européens : l’OL (classement moyen 2nd) et l’OM (classement moyen 5ème). Le PSG figure à la 6ème place, principalement du fait d’une période post-Qatari peu fructueuse, 9ème voire 8ème sur les périodes 2002/2003 à 2011/2012 puis 1er depuis.

Parmi les clubs montant de ces dernières années, on peut remarque Nice ou encore Saint-Etienne, habitués de la seconde partie de tableau avant 2012/2013 et qui se sont stabilisés depuis sur la première. Mais aussi Reims, en ligue 2 sur les dix premières années puis 15ème sur la période 2012-2017 et 8ème sur la période 2017-2019.

A contrario, des clubs comme Ajaccio, Evian, Lorient, Nancy, Sochaux et Valenciennes ont réussi à survivre de nombreuses saisons avant de dégringoler au classement d’année en année pour finir en L2. Le destin tragique de Caen, qui progressait sur les 15 premières saisons et qui a finalement chuté en L2 sur les deux dernières.

• Evolution du classement sur une saison

On regarde ici le lien entre le classement aux différentes journées de la saison avec le classement final à la 38ème.

En catégorisant le classement en 6 classes : premier, qualifié en C1, qualifié en EL, non européen mais finissant dans la première partie du championnat, seconde partie du championnat mais non relégable et relégable, on se rend compte qu’à mi-parcours du championnat, la moitié des équipes sont déjà dans la portion du classement qui correspondra à celle de la 38ème journée. C’est à partir de la 30ème journée que les trois quarts des équipes sont déjà à leur positionnement final. En se basant sur cette approche, il en ressort qu’entre la 33ème journée et la 35ème journée, ne se joue que 20 % du championnat et qu’à l’avant-dernière, c’est 9 % des équipes qui vont être impactée par les résultats des derniers matchs.

En privilégiant une approche moins qualitative mais directement sur les classement aux différents moments de la saison, le coefficient de corrélation (de Spearman) montre que c’est à partir de la 12ème journée que le lien devient statistiquement significatif () et se renforce nettement après les résultats de la 16ème journée (). il faut alors attendre les résultats de la 26ème journée pour atteindre une corrélation quasi-parfaite ().

Au final, les clubs doivent, certes, faire preuve de régularité pour conserver les meilleures places mais aussi se positionner assez rapidement dans la saison. L’histoire un peu trop belle du club rattrapant sa saison sur la seconde partie de saison après avoir loupée la première n’est pas une chimère… mais finalement assez rare.

• Probabilité de passer d’une catégorie de classement à une autre

Le tableau ci-dessous présente les probabilités de changer de zone du classement en fonction des temps suivants : 10ème journée, 20ème journée et 30ème journée. 

On constate qu’à mi parcours (20ème journée), le premier du championnat a  60 % de chance de finir 1er en fin de saison. Evidement cette probabilité prend en compte l’historique depuis le passage du championnat à 20 clubs et néglige la suprématie actuelle du PSG sur le championnat. On peut en conclure qu’il fut une époque où le titre de champion se jouait sur la seconde partie de saison et non dans les deux premiers tiers du championnat. Le titre étant visiblement joué à partir de la 30ème, toutes les équipes premières à ce moment de la saison l’ont également été en fin de saison.

A la 20ème journée, les second et troisième ont une chance sur deux de se qualifier en ligue des champions mais aussi 25 % de retomber en Europa League et 10 % de perdre les avantages offerts par une première partie de saison rayonnante. Les quatrième et cinquième, quant à eux, ont 35 % de chance de se qualifier en Europa League, 25 % en C1. Dans 35 % des cas, ces équipes ont finalement terminé hors de la zone européenne et dans 15 % des cas, dans la seconde partie de tableau.

Constat inverse, les équipes en première partie de tableau à mi-parcours ont 14 % de chance de finir européen, et celle en seconde partie de tableau hors relégable, 4 %.

Important, être dans la première moitié de championnat à la 20ème journée, anéantit le risque de finir relégable à la fin de la saison. Evidemment, constat différent pour les équipes qui sont alors relégable à ce moment de la saison mais positionnées dans la seconde partie de tableau, ils ont un risque de 17 % de finir en L2 à la 38ème journée. Quant à celles qui sont déjà dans la zone rouge, dans 60 % des cas elles échouent à s’en sortir et ne peuvent prétendre au mieux qu’à en sortir et à rester dans la seconde partie de tableau. L’espoir réside tout de même pour ces équipes qui à la 30ème journée sont en position de relégation, 16 % arrivent à s’en dégager avant la clôture de la saison et 3 % ont réalisé l’exploit d’inverser la tendance en finassant dans la première partie de championnat mais non européen.

• Temps de survie en L1

Le graphique suivant présente les temps de survie des clubs de L1 (ALL représente toutes les équipes, L1 représente les clubs hors promus) et de ceux promus (P1 correspondant à l’équipe qui a fini premier de L2 la saison précédente, P2 second et P3 troisième).

Le temps de survie des clubs est en moyenne de 4 saisons. En fonction du statut de départ du club l’indicateur évolue nettement.

Ainsi, les clubs qui étaient en L1 au démarrage de la série de données ont un temps de survie de 9 saisons. On peut même constater que ceux qui ont réussi à se maintenir en L1 pendant 10 saison ont assuré leur survie sur les 7 dernières. Les promus ont une survie trois fois inférieure à ces clubs.

Les clubs qui avaient remporté la L2 la saison précédente ont un meilleur taux de survie que les autres : 4 saisons. Néanmoins, ils n’ont jamais réussi à se maintenir en L1 sur le très long terme. Même si leur temps de survie est plus faible, 3 saisons, paradoxalement ce sont les clubs qui avaient fini 3ème en L2 qui ont le plus de chance de stabiliser en L1.  Enfin, le second connait les mêmes difficultés que les 1er de L2 avec un temps de survie encore plus faible qui soit observé : 2 saisons.

Profils

Etant donné l’amas de variables considérées, on ne présentera pas la projection des modalités de variables de l’ACM mais uniquement les quatre profils qui en ressortent.

Les deux premiers profils qui s’opposent le plus fortement :

• Le profil des clubs relégables en fin de saison,
  • Classé en seconde partie de tableau à la 10^ème journée puis en position de relégation à la 20^ème et la 30^ème ;
  • Age moyen de l’équipe compris entre 24,1 et 26,4 ans / un effectif de 31 à 33 joueurs / 17 à 19.5 joueurs étrangers dans l’équipe ;
  • Un budget compris entre 13 et 30 Me / un stade de 18 523 à 26 390 places ;
  • 42 à 49 points ;
  • 10 à 13 matchs gagnés par saison et 10.5 à 12 matchs nuls / 10,5 à 12 matchs nuls ;
  • Inscrire entre 27 et 45 buts et une différence de but comprise entre -55 et -14 ;
  • Buts marqués : 0 à 1 sur CSC / 10 à 27 dans le jeu ;
  • Cartons reçus : Entre 5 et 14 pour comportement antisportif / 1 à 4 pour simulation / 12 et 15 pour raison « autres » ;
  • Subis par match : 2 à 4 ballons en profondeurs / 4 à 11 contre-attaques / 13 à 21 coups de pied arrêté / 22 à 30 centres / 59 à 61.5 longs ballons / 13,1 à 16,9 tirs  ;
  • 47 à 49.55 % de possession de balle / un jeu orienté sur l’aile droite dans 36 à 38 % des cas / 26 à 32 % d’actions dans la zone défensive / 42 à 45 % dans la zone du milieu de terrain ;
  • 44 à 54 % de tirs à l’extérieur de la surface, 39 à 47 % dans les 18 mètres , 2 à 5 % dans les 6 mètres, 52 % à 60 % du milieu de terrain ;
  • Réussir par match : 3.8 à 6.4 dribbles / 15.3 à 19.4 fautes défensives / 18.65 à 24.9 interceptions défensives / 236 à 348.5 passes courtes / 65.2 à 77.05 % de passes / 10,5 à 24 tacles défensifs / 3,7 à 4,05 tirs cadrés  ;
  • 0 à 2 pénaltys obtenus.

• Le profil des clubs qualifiés en EL ou qui gagne le championnat,
  • Etre classé entre la 10^ème et la 4^ème place à la 10^ème journée de championnat et à la 20^ème / entre la 5^ème et 4^ème place à la 30^ème journée; 
  • Age moyen de l’équipe compris entre 21,1 et 23,3 ans / un effectif de 37 à 57 joueurs ;
  • Un budget compris entre 69 et 557 Me / un stade de 38 0004 à 67 395 places ;
  • Gagner entre 10,5 et 17 matchs à domicile / 5 et 15 matchs à l’extérieur ;
  • Cartons reçus : 0 pour simulation / 4 à 5 pour comportements antisportifs  / 17 à 31 pour raison « autre » ;
  • Avoir inscrit entre 31 et 70 buts à domicile / 19 et 49 buts à l’extérieur ;
  • Avoir encaissé entre 7 et 20 buts à domicile / 7 et 23 buts à l’extérieur ;
  • Subir par match : 0 à 1 ballon en profondeur / 3 et 8 CPA / 14 et 19 centres / 9 à 10,8 tirs par match ;
  • Avoir une possession comprise entre 49,55-52 % / un jeu utilisant le côté droit dans 32 à 36 % des cas / 22 % à 26 % d’actions dans la zone défensive / 46 à 51 % dans la zone du milieu / 51 à 71 % de tirs dans les 18 mètres ;
  • 7 à 22 % de tirs dans les 6 mètres / 13 à 40 % de tirs de la surface / 65 à 71 % depuis le milieu de terrain ;
  • Réussir par match : Entre 12,35 et 15,55 duels aériens gagnés / 9,65 à 16,8 dribbles offensif / 10.4 à 12.9 fautes défensives / 8,8 à 13,45 interceptions défensives / 348,5 à 675 passes courtes / 77,05 et 89,6 % passes / 18 à 19,3 tacles défensifs  ;
  • Avoir encaissé entre 22 et 28,5 buts dans le jeu / entre 4 et 5 pénaltys dans la saison ;
  • Avoir inscrit 2 à 8 buts sur CSC / 33,5 à 79 buts dans le jeu / 5 et 13 buts sur penalty.

Le profil des clubs qui terminent en EL et de ceux qui remportent le championnat semblent assez proches. Les deux prochains profils opposent fortement les qualifiés en C1 et finissant en première partie de tableau sans être européen à ceux finissant en seconde partie de tableau sans finir relégable.

• Le profil des clubs en seconde partie de tableau sans être relégable,
  • Etre relégable à la 10^ème journée / en seconde partie de tableau à la 20^ème et à la 30^ème ;
  • Age moyen de l’équipe entre 23,3 et 24,1 ;
  • Un budget compris entre 30 et 40 Me / un stade de 3 200 à 18 523 ;
  • 18 à 42 points / 12 à 19 nuls / 14 à 26 matchs perdus ;
  • Une différence de but comprise entre -14 et -4 ;
  • Gagner au total entre 3 et 10 match / 1 à 8 à domicile  / 1 à 5 à l’extérieur;
  • Encaisser 47 à 83 buts au total / 20 à 37 buts à domicile / 27 à 49 à l’extérieur ;
  • 0 à 1 buts encaissés sur contre-attaque ;
  • Buts encaissés : 28,5 à 57 dans le jeu / 5 à 12 buts sur pénalty ;
  • Inscrire 13 à 31 buts à domicile / 5 à 19 à l’extérieur ;
  • Duels aériens gagnés entre 15,55 et 23,1 par match ;
  • Subir par match : 20 à 22 centres / 61,5 à 77 longs ballons / 361 à 489 passes courtes / 10,8 à 13,1 tirs ;
  • Cartons : 0 à 2 pour comportements antisportifs / 15 à 17 pour motif « autre »;
  • Une possession de 42,3 à 47 % / un jeu côté gauche dans 37 à 46 % / axé au milieu dans 19 à 25 % ;
    
  • Réussir par match : 7,85 à 9,65 dribbles offensifs /  12,9 à 14 fautes défensives / 9,6 à 13,35 fautes offensives / 13,45 à 16,05 interception défensives / 0 à 1 ballon en profondeur réussies / 11 à 20 centres / 66 à 81 long ballons / 2.6 à 3.7 tirs cadrés par  / 15,5 à 18 tacles défensifs ;
  • 54 à 80 fautes ;
  • 0 à 1 buts inscrits sur contre-attaque /  1 à 8 buts inscrits sur CPA ;
  • 2 à 4 pénalty obtenus.

• Clubs qualifiés en C1 ou en première partie de tableau mais non européen,
  • Un effectif de 27 à 31 joueurs ;
  • Positionné en C1 sur les 10^ème, 20^ème et 30^ème journée voire en première partie de tableau sur cette dernière période ;
  • 60 à 96 points / 16 à 30 matchs gagnés / 2 à 10 matchs perdus  ;
  • Une différence de but comprise entre +11 et +83 ;
  • 19 à 41 buts encaissés / 10 à 22 buts encaissés dans le jeu ;
  • Subir par match : 252 à 361 passes courtes / 13,35 à 18.2 fautes offensives ;
  • Réussir par match : 8,1 à 12,35 duels aériens gagnés / 35 à 54 fautes commises / 2,5 à 3,8 hors jeu / 4,65 à 6,7 tirs cadrés / 13 à 17,7 tirs tentés / 20 à 29 centres tentés / 36 à 58 long ballons / 2 à 7 ballons en profondeurs ;
  • 52 à 63,4 % de possession de balle / 28 à 31 % d’actions dans la zone offensives ;
  • 5 à 7 % de but dans les 6 mètres ;
• • Un jeu équilibré entre le côté gauche (29 à 35 %) et le milieu (27 à 33 %) ;
  • 0 à 3 pénalty pris ;
  • 3 à 14 buts inscrits sur contre-attaque par match / 13 à 26 buts sur CPA ;
  • 0 à 1 carton obtenu pour simulation ;
  • Avoir le meilleur buteur et le meilleur passeur.

A noter que le positionnement des clubs en première partie de tableau non européen demeure proche de l’origine du repère. Marquant le fait que ces équipes, même si elles parviennent à se hisser dans cette zone du classement, ont des caractéristiques mixtes avec les autres profils.

Facteurs de chance et de risque

Pour conclure, on cherche à caractériser les facteurs de chance de finir européen en fin de saison et de risque de finir relégable.

• Facteur de chances de finir européen en fin de saison (C1 ou EL)

Le filtre différentiel met en évidence le panel de variables suivants liés au fait de finir européen en fin de saison :

En lançant la procédure de sélection des variables pour une approche multivariée via modèle logistique, il ressort que les variables suivantes sont très fortement liées à ce que l’on cherche à discriminer :  

• Les équipes comptant dans leur rang le meilleur buteur du championnat ont 100 % de chance de finir européen, 11 % pour les autres ;
• Les équipes qui ont un ratio de tirs cadrés par match supérieur à 4,65 ont 50 % de chance de se qualifier pour l’une des deux compétitions européennes, en dessous le taux est inférieur ou égal à 8 % ;
• Les équipes qui réussissent plus de 385 passes courtes par match ont 45 % de chance de finir européenne, en dessous leur chance sont nettement plus faible, inférieure ou égale à 14 %.

Par souci de convergence du modèle, ces trois informations ont été retirées. Le modèle optimal se base alors sur les quatre variables suivantes :

Sur ces quatre variables, seulement trois sont interprétables (p < 0,1). Ainsi, les équipes qui ont un taux de tirs cadrés par match compris entre 13 et 17,7 ont 9,6 fois plus de chance de finir européen vis à vis de celles qui ont un taux compris entre 65,2 et 74,4. Les équipes qui ont un pourcentage de passes réussies compris entre 80,05 et 89,6 % ont 8,3 fois plus de chance que celles qui ont un taux compris entre 65,2 et 74,4 %. Enfin, les équipes qui réussissent 2 à 7 ballons en profondeur par match ont 2,3 fois plus de chance de finir européen que celles qui en réussissent au plus 1.

• Facteur de risque de finir relégable

Le filtre différentiel met en évidence le panel de variables suivants liées au fait de finir relégable en fin de saison :

En lançant la procédure de sélection des variables pour une approche multivariée via modèle logistique, il ressort que les variables suivantes sont très fortement liées à ce que l’on cherche à discriminer :  

• Les équipes qui ont un taux de possession de balle inférieur à 47 % ont 42 % de risque de finir relégable. 16 % pour celles ayant un taux compris entre 47 % et 49,55 % et inférieur à 2 % après ;
• Les équipes réussissant moins de 21,5 passes dans le jeu par match ont 40 % de risque de finir relégable. 15 % pour celles comprises entre 21,5 et 27, inférieurs à 4 % au delà ;
• Les équipes faisant moins de 11,8 tirs par match ont entre 24 % et 27 % de finir relégable. 8 % pour celles comprises entre 11,8 et 13 et 0 % pour celles au delà de 13.

Par souci de convergence du modèle, ces trois informations ont été retirées. Le modèle optimal se base alors sur les deux variables suivantes :

Sur ces deux variables, seulement une est interprétable (p < 0,5). Ainsi, les équipes qui réussissent entre 236 et 314 passes courtes par match ont 31,2 fois plus de risque de finir en L2 que celles qui en réussissent plus de 385. Même si la p-valeur n’est pas significative (non rejet de l’unité), celles qui réussissent entre 314 et 348.5 passes courtes ont 7,6 fois plus de risque de finir en L2. De même pour les buts sur contre-attaque qui semble être une variable discriminante, les équipes qui en réussissent au plus 3 ont 4,25 fois plus de risque d’échouer en fin de saisons que celles qui en réussissent au moins 5.

 

Chronologie d’une discipline passionante

Construire une chronologie de cette discipline qu’est la statistique et la modélisation est particulièrement compliquée. Si l’on voudrait être exhaustif, il faudrait si prendre selon les trois axes suivants:

• Les praticiens qui ont prouvé l’apport des outils statistiques dans l’évolution du monde d’aujourd’hui ;
• Les théoriciens de la probabilité et de la statistique dont les travaux ont élaboré les outils tel qu’on les connaît ;
• De manière plus global, les mathématiciens dont l’agrégat des innovations ont permis aux spécialistes de la probabilité et la statistique de développer leurs outils.

En outre, tenir une liste leur rendant grâce à tous n’est donc pas si aisé. Ce milieu manquant cruellement de visibilité, on aura vite fait d’en oublier un très grand nombre.

La chronologie ci-dessous tente (en vain il faut le reconnaître) de donner un aperçu de l’évolution de cette discipline. Elle sera complétée au fur et à mesure tant le travail qu’elle nécessite demeure énorme. N’hésitez pas à me reprendre ou mettre en évidence des oublis fondamentaux afin de m’aider à construire la chronologie la plus pertinente qui soit.

Mayotte en chiffres

Présentation et démarche

On présente ici deux analyses : celles des données du recensement de la population de 2012 puis de l’indice des prix mensuellement actualisé. Les variables sont directement récupérables sur le site de l’Insee. Pour le premier volet, on se restreindra à une approche commune en attendant une remise à plat du projet en fin d’année, qui s’orientera également vers une approche temporelle grâce aux données de 2017 publiées entre temps. De même pour le second volet, s’arrêtant à 2017 alors que les indicateurs sont publiés en continue jusqu’à aujourd’hui.

Un mot essentiel, la remise en question des données de l’Insee en France est assez coutumière, mais il est vrai qu’à Mayotte cela dépasse clairement l’entendement. L’Insee a pris le temps de publier sous format blog une discussion particulièrement intéressante de chaque argument sur lesquels elle est remise en question, malheureusement on entend encore des nombreux hauts placés les remettre en question. En fouillant un peu, en cherchant à être complémentaire au travail déjà produit et en imaginant que le débat soit fondé, on est alors heureux d’apprendre qu’à Mayotte, d’après ces hauts placés, il n’y a pas de sur-fécondité, pas de sur-mortalité, par de sur-recours aux pathologies infectieuses et encore plus fort, pas de sur-délinquance, etc. bref qu’à part un déficit de volume d’effectifs, déjà démontré avec les données de l’Insee, finalement tout va bien. Car « oui », dire que l’on est le double de ce que l’Insee avance, c’est diviser par deux fois plus chaque indicateur, l’exercice étant fait, voilà le constant que l’on en déduit. Cet effet est d’autant plus étonnant que les publications de l’Insee ne cesse de tirer la sonnette d’alarme sur la situation depuis plusieurs années, du point de vue de l’auteur de ce site, c’est une façon assez peu conventionnelle et extraordinaire de tirer sur l’un des défenseurs les plus pertinents et écoutés en France, mais bon comme l’a si bien dit son Directeur Général :

« On s’attaque au thermomètre plutôt qu’à la maladie »

Le raisonnement par l’absurde étant désormais fait, on partira du principe que les données de l’Insee sont fiables et que le projet proposé ici a un sens autant théorique que contextuel.

Ahhhhhh… Mayotte

Le territoire de Mayotte est une île mesurant 376 km2 et se situe géographiquement dans l’archipel des Comores, lui-même situé dans l’océan Indien. Elle se divise en deux îles principales nommées la Grande-Terre et la Petite-Terre (oui bah l’une est plus petite que l’autre).

Historiquement, Mayotte était un territoire autonome jusqu’en 1841, date à laquelle le sultan prend la décision de vendre l’île à la France du fait de la pression des territoires voisins. Mayotte devient ainsi française en 1848. L’île, qui n’a jamais appartenu aux Comores donc, maintient ce premier statut suite à un vote ultra-majoritaire en 1976. Toujours sur la demande de sa population, elle vote majoritairement pour devenir un département d’Outre-mer français en 2009 et accède au statut de zone ultrapériphérique de l’Union Européenne en 2014. Remettre en question l’appartenance de Mayotte à la France, peut revenir d’une certaine manière à remettre en question celle de ma bien-aimée Corse ou même, pourquoi pas, de l’Alsace et la Lorraine, après tous les Mahorais sont français depuis plus longtemps que certains territoires rattachés à l’Hexagone directement…

Le territoire de divise en 17 communes, se déclinant en 72 villages. La commune de Mamoudzou rassemblant la plus grande partie de la population de Mayotte, elle figure comme la capitale économique de l’île.

Synthétiquement sur le plan socio-démographique, on rappellera qu’il s’agit du département le plus jeune de France avec un habitant sur deux âgé de 17 ans ou moins. Environ la moitié des habitants est de nationalité étrangère, dont la moitié en situation irrégulière, représentant un volume de tout de même près de 100 000 personnes alimentant ainsi le folklore local que l’on connait. Le contexte global tourne autour de la précarité avec quatre logements sur dix en tôle, trois sur dix n’ont pas accès à l’eau courante et les trois quarts de la population vivant en deçà du seuil de bas revenus métropolitains. L’Illettrisme concerne un habitant sur trois, seulement une personne sur quatre de 15 ans ou plus sort du système scolaire avec un diplôme qualifiant. Enfin, le secteur tertiaire est le plus représenté sur le territoire (concerne huit habitants sur dix) et plus précisément un habitant sur deux travaille dans la fonction publique.

Toujours le plus synthétiquement possible et sur le plan sanitaire cette fois-ci, le territoire est sujet à de nombreuses épidémies chaque année, à minima une par an depuis quelques temps. A cela s’ajoute un fort déficit en professionnels de santé et donc défaut de prise en charge, expliquant (de par bien d’autres indicateurs) qu’une personne née à Mayotte a globalement dix années de vie en moins qu’en France Hexagonale. Les données sur l’environnement sont assez faiblardes et on serait curieux de voir ce qu’elles pourraient offrir au diagnostic en Santé de Mayotte. En terme de pathologie, le diabète est particulièrement présent, tout comme les maladies infectieuses. On s’arrêtera là, très sincèrement, sur le plan Santé, tout est plus haut qu’en il ne le faut pas et plus bas quand il ne le faut pas qu’ailleurs.

Enfin, sur le plan sécuritaire, qui touche terriblement ce bout de territoire qui, il y a encore une vingtaine d’années était l’un des derniers paradis de la surface du globe provoquant un véritable phénomène dépressif à l’idée de le quitter, depuis 2011 la situation ne cesse de s’empirer sur cet aspect. Vivre à Mayotte est tristement devenu pénible et l’on espère de tout cœur que les mouvements sociaux en cours permettront à l’île de partir sur une nouvelle dynamique positive car, réellement, ce département est magnifique doublée d’une richesse culturelle incroyable et mériterait d’être un développement à l’aune de toutes ses qualités.

On pourra retrouver les éléments plus complets ayant alimenté ce micro-diagnostic subjectif de Mayotte ici :

https://www.mayotte.ars.sante.fr/le-panorama-sante-de-lars-mayotte

, le document reprenant en plus tout le volet bibliographique présenté initialement ici et supprimé depuis. A compléter avec la page wikipedia :

https://fr.wikipedia.org/wiki/Mayotte

Exploitation des données du recensement de la population de 2012

Les données : https://www.insee.fr/fr/statistiques/2409395?sommaire=2409812

Les données utilisées sont celles du recensement de la population de 2012 à l’échelle de la commune et sont donc déclaratives. Une base de données de 118 variables peut être construite, que l’on ramène à 86 variables optimisées en fonction de la taille de l’effectif ventilé sur les variables d’origines. Étant donné que l’on se lance dans une étude typologique, avec pour objectif de montrer la ressemblance entre les différentes communes, on a considéré la part en pourcentage de la ventilation des différents champs au sein des différentes thématiques pour chaque commune prise individuellement (en somme, une ligne équivaut à une commune). En effet, considérer les effectifs bruts ou bien la part en pourcentage en fonction des totaux mène à des résultats biaisés par le fait qu’il est évident que plus une commune concentre d’individus et de ménages et plus ses effectifs seront grands.

Deux types de données sont regroupées, celles issues du bulletin individuel et celles issues de la feuille logement.

• Pour les premières on trouve :

– La répartition par classes d’âge en sept catégories (0-4 ans, 5-19 ans, 20-29 ans, 30-39 ans, 40-49 ans, 50-64 ans et 65 ans ou plus) ;

– La répartition par genre ;

– La répartition par nationalité (français, étranger) ;

– La répartition par lieu de naissance (né à Mayotte, né ailleurs en France, né à l’Étranger) ;

– La répartition selon le statut matrimonial (célibataire-veuf-divorcé, marié) chez les 15 ans ou plus ;

– La répartition en fonction d’être en couple ou non chez les 15 ans ou plus ;

– La répartition en fonction du logement antérieur à Mayotte ou non ;

– La répartition selon la Catégorie Socio-professionnelle (CSP), au sens du recensement et non du Bureau International du Travail (BIT), renseignée chez les 15 ans ou plus (a un travail, chômeur, étudiants, retraité-au foyer-autres inactifs) ;

– La répartition selon le niveau de diplôme chez les 18 ans ou plus (sans scolarité, sans diplôme, CEP-BEPC-CAP-BEP, BAC-BAC pro, diplôme du premier cycle, diplôme du second ou troisième cycle).

• Et enfin, pour les données issues de la feuille de logement :

– La répartition par catégorie de logement (résidence principale, résidence vacante, logement secondaire-occasionnel) ;

– La répartition par aspect du bâti (habitation de fortune, habitation en dur, habitation traditionnelle-en bois) ;

– La répartition par type de construction pour les résidences principales (individuel, collectif) ;

– La répartition par statut d’occupation pour les résidences principales (propriétaire du logement uniquement, propriétaire du logement et du sol, locataire, logé gratuitement) ;

– La répartition par nature du sol pour les résidences principales (en terre battue, en béton, carrelage) ;

– La répartition par nombre de pièces pour les résidences principales (1 pièce, 2 pièces, 3-4 pièces, 5 pièces ou plus) ;

– La taille des ménages pour les résidences principales ;

– La répartition selon l’accessibilité par véhicule pour les résidences principales ;

– La répartition selon le nombre de voitures pour les résidences principales (aucune, une voiture, deux ou plus voitures) ;

– La répartition selon la présence ou non du confort de base pour les résidences principales (un logement est classé comme ayant le confort de base s’il a les WC, la baignoire, l’électricité et l’eau à l’intérieur du logement, si un seul de ces 4 items manque alors le logement est classé sans confort) ;

– La répartition selon le type d’accès à l’eau pour les résidences principales (eau froide à l’intérieur du logement seulement, eau froide et chaude à l’intérieur du logement, absence d’eau à l’intérieur et accès via une BFM, absence d’eau à l’intérieur et accès via un autre moyen qu’une BFM) ;

– La répartition selon la présence ou non de WC pour les résidences principales,

– La répartition selon la présence ou non d’électricité pour les résidences principales ;

– La répartition selon la présence ou non de baignoire pour les résidences principales ;

– La répartition selon le type d’évacuation des eaux usées pour les résidences principales (par le sol, par les égouts, par une fosse septique ;

– La répartition selon la présence ou non de bacs à ordure pour les résidences principales ;

– La répartition selon le mode de cuisson des aliments pour les résidences principales (cuisson par feu de bois, cuisson par réchaud à pétrole, gazinières, autres modes de cuisson) ;

– La répartition selon la présence ou non d’ordinateur pour les résidences principales ;

– La répartition selon la présence ou non de téléviseur pour les résidences principales ;

– La répartition selon la présence ou non de réfrigérateur pour les résidences principales ;

– La répartition selon la présence ou non de congélateur pour les résidences principales ;

– La répartition selon la présence ou non de lave-linge pour les résidences principales.

Cet inventaire est à garder à l’esprit pour les analyses à venir, car c’est à travers ce sous-ensemble de variables que l’on établira les différentes typologies. Évidemment, la considération d’autres caractéristiques amènerait à des résultats sensiblement différents, toutefois il est bon de savoir que l’on a là toutes les données socio-démographiques de base permettant d’ériger un distinguo « communes dans une situation globalement précaire » versus « communes plus développées ».

L’Analyse :

L’étude se déroulera en deux étapes :

– La première étape consistera à procéder à une analyse exploratoire bivariée en faisant le point sur les corrélations entre les différentes variables au travers des coefficients de corrélation de Pearson, Spearman et Kendall puisque l’on a un jeu de données au format exclusivement continue et que de taille d’effectifs reste assez faible () ;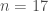

– La seconde étape sera axée sur une étude typologique multivariée au travers d’une Analyse en Composantes Principales (ACP) et d’une Classification Ascendante Hiérarchique (CAH) afin de regrouper les communes en fonction des différents profils que l’on pourra mettre en évidence.

• L’Analyse bivariée

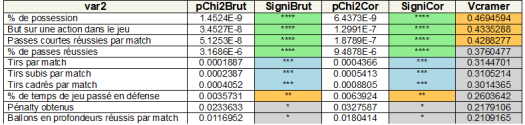
Donc on commence par la première phase des analyses. On lance sur l’ensemble des combinaisons, de 2 variables d’intérêt parmi les 86 variables présentes, le calcul des coefficients de corrélation cités ci-dessus, ce qui donne 3 655 combinaisons à éplucher. Le graphe ci-dessous présente le nombre de liaisons qui ressortent en fixant un ,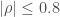

En résumé sur l’ensemble des combinaisons et selon le seuil fixé, on a 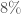de corrélations significatives selon le coefficient de corrélation de Pearson, 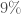selon celui de Spearman et selon celui de Kendall. Face à autant de corrélations à parcourir, il convient de focaliser sur certaines variables importantes et partir du principe que l’on aura une vue plus exhaustive lors de l’approche multivariée. Ainsi, six thématiques sont jugées intéressantes, les croisements : avec l’âge, le genre, l’accès à l’eau, la CSP, la nationalité et le confort des logements.

Pour les corrélations avec l’âge, quatre classes d’âges ressortent dans l’analyse bivariée. Les quatre figures qui suivent présentent les interactions avec la valeur du coefficient entre parenthèse et le sens de la corrélation (flèche) :

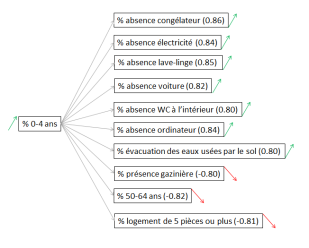
Globalement, la part des 0-4 ans croît avec celles du manque d’équipement et de la taille du logement. Assez logiquement, plus la part d’enfants en bas âge augmente et plus la part des personnes âgées diminue.

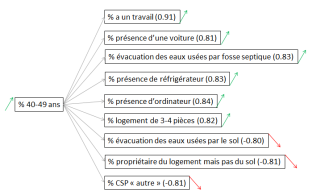
Globalement, la part des 40-49 ans croît en même temps que celles des conditions de vie et notamment le fait de travailler.

Globalement, la part des 50-64 ans croît en même temps que celles des équipements du ménage, des diplômés du BAC ou d’un BAC professionnel et du nombre de français.

Globalement, la part des 65 ans ou plus croît en même temps que celles des français et de ceux ayant l’eau froide seulement à l’intérieur du logement. A contrario, les parts des modes de cuisson par réchaud à pétrole et des étrangers diminuent quand elle augmente.

Pour les corrélations avec le genre, aucun croisement ne ressort, à la différence de l’accès à l’eau pour la part de ménages ayant seulement l’eau froide à l’intérieur du logement et pour celle des ménages s’approvisionnant en eau par un autre moyen que les BFM. Les deux figures qui suivent présentent les interactions avec la valeur du coefficient entre parenthèse et le sens de la corrélation (flèche) :

Globalement, la part des ménages avec seulement l’eau froide à l’intérieur du ménage croît en même temps que la qualité et la taille du logement.

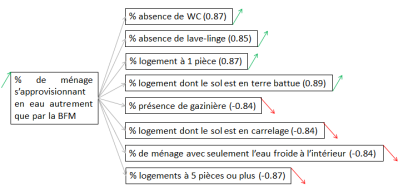
Globalement, la part des ménage s’approvisionnant en eau autrement que par la BFM croît en même temps que celles des logements précaires.

Pour les corrélations avec la CSP, deux catégories ressortent dans l’analyse bivariée, la part de ceux qui ont un travail et celle de ceux de CSP « autre » (retraité, au foyer, autres inactifs). Les trois figures qui suivent présentent les interactions avec la valeur du coefficient entre parenthèse et le sens de la corrélation (flèche) :

Globalement, la part de ceux qui ont un emploi croît avec celles des équipements du ménage ainsi que celle des 40-49 ans. De plus, elle est corrélée avec le niveau scolaire.

Globalement, la part de ceux ayant une CSP catégorisée « autre » croît avec l’absence d’équipements et de diplôme qualifiant. De plus, lorsque la part augmente, celles des 40-49 ans et 50-64 ans diminuent.

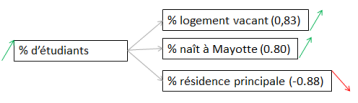
Globalement, la part d’étudiants croît en même temps que la part des catégories de logement et la part de nés à Mayotte.

Pour les corrélations avec la nationalité, les deux catégories ressortent dans l’analyse bivariée. Les deux figures qui suivent présentent les interactions avec la valeur du coefficient entre parenthèse et le sens de la corrélation (flèche) :

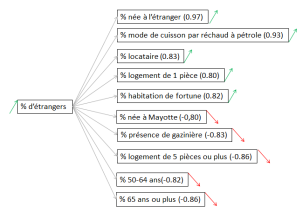
Globalement, la part des étrangers croît avec celles des logements précaires et de locataires. De plus, quand elle augmente, celles des 50-64 ans et des 65 ans ou plus diminuent.

Globalement, la part des français croît avec celles des logements de bonnes qualités. De plus, elle croît avec celles des 50-64 ans et des 65 ans ou plus.

Pour les corrélations avec le confort du logement, les deux catégories ressortent dans l’analyse bivariée. La figure qui suit présente les interactions avec la valeur du coefficient entre parenthèse et le sens de la corrélation (flèche) :

Globalement, l’indicateur du manque de confort reste assez robuste puisque, même s’il est basé sur uniquement quatre caractéristiques (WC à l’intérieur, baignoire, électricité, eau à l’intérieur), on voit que la part croît avec celles de l’absence de plusieurs autres équipements. De plus, quand elle augmente, celle des diplômés du BAC ou du BAC professionnel diminue. On notera que l’on ne présente pas l’analyse des corrélations avec la part des logements avec confort car elle conduit aux mêmes résultats inversés.

• L’Analyse multivariée

La seconde étape consiste donc à procéder à une analyse exploratoire multivariée au travers d’une ACP. Dans un premier temps, on détermine le nombre de composantes factorielles à retenir, on obtient alors le graphe de l’évolution des parts de variance suivant,

On constate que si on se limite aux deux premiers axes factoriels, c’est 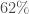de la variance que l’on restitue. Pour une ACP cela  semble un peu faible malgré le coude que l’on observe. Cependant, si on souhaite atteindre le gap classique de plus de 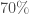, on est obligé d’aller jusqu’à quatre axes factoriels, complexifiant un peu trop la lisibilité pour un gain plutôt limité. Afin de déterminer si on peut se limiter à deux composantes, on prend le temps de voir quelles oppositions chaque composante offre. On fixe le critère de significativité pour un coefficient sur la composante supérieur à 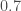ou inférieur à .

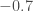Pour la première composante, on constate l’opposition entre :

– La part des 40 à 64 ans, de ceux qui ont un emploi, de ceux ayant un BAC ou un BAC professionnel, de ceux ayant un diplôme du premier cycle, des logements en dur, des logements équipés d’un carrelage, des logements de trois pièces ou plus, des ménages avec une voiture, des logements catégorisés comme confortable, des logements équipés en WC, baignoire, électricité, ordinateur, téléviseur, réfrigérateur, congélateur, lave-linge et des logements dont l’évacuation des eaux usées se fait par fosse septique.

Soit des logements de bonnes qualités avec une population âgée qui travaille et est diplômée.

– Et la part des 0 à 4 ans, des CSP « autre » (retraité, au foyer, autres inactifs), des non scolarisés, des logements dont le sol est en terre, des logements de 1 à 2 pièce(s), des ménages sans voiture, des logements sans confort, des logements dont l’accès à l’eau se fait hors de la maison et pas par la BFM, des logements sans WC, sans électricité, sans baignoire, sans ordinateur, sans téléviseur, sans réfrigérateur, sans congélateur, sans lave-linge, dont l’évacuation des eaux usées se fait par le sol et dont le mode de cuisson se fait par le bois.

Soit des logements de mauvaise qualité, regroupant une grande part de jeunes enfants et d’une population en CSP « autre » et non scolarisée.

Pour la seconde composante, les oppositions sont déjà beaucoup moins nombreuses :

– La part des étrangers, de ceux nés à l’étranger, de ceux dont le logement antérieur n’était pas en France, de ceux ayant un diplôme du second ou troisième cycle, des locataires, de ceux ayant l’eau froide et chaude à l’intérieur du logement.

Soit une population étrangère diplômées et ayant un niveau de vie supérieur à la moyenne.

– Et la part des français, nés à Mayotte, dont le logement antérieur était à Mayotte, des étudiants et des logements vacants. Soit la population jeune et la population mahoraise.

Pour la troisième composante, on ne compte plus qu’une seule opposition significative : les logements collectifs versus les logement individuelles. Et pour la quatrième composante, aucune.

Ce premier bilan permet d’argumenter le choix de se restreindre à uniquement deux composantes étant donné que les composantes 3 et 4 n’apportent que peu d’information.

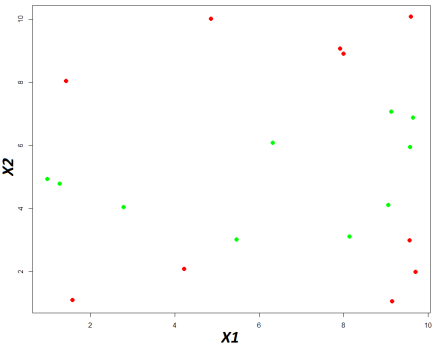
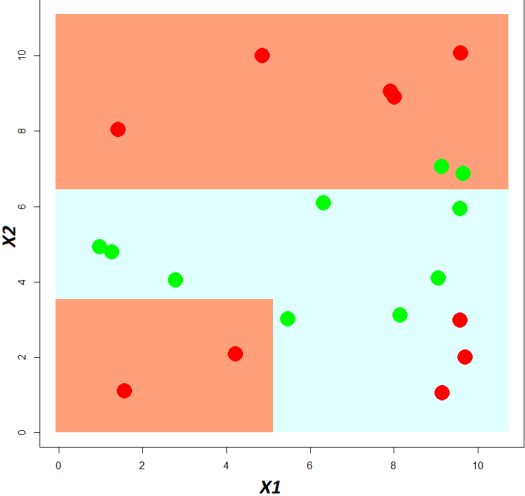
La figure ci-dessous présente la projection des variables sur les deux composantes retenues. En haut la projection de base et en bas le travail d’interprétation que l’on ajoute sur la figure de base :

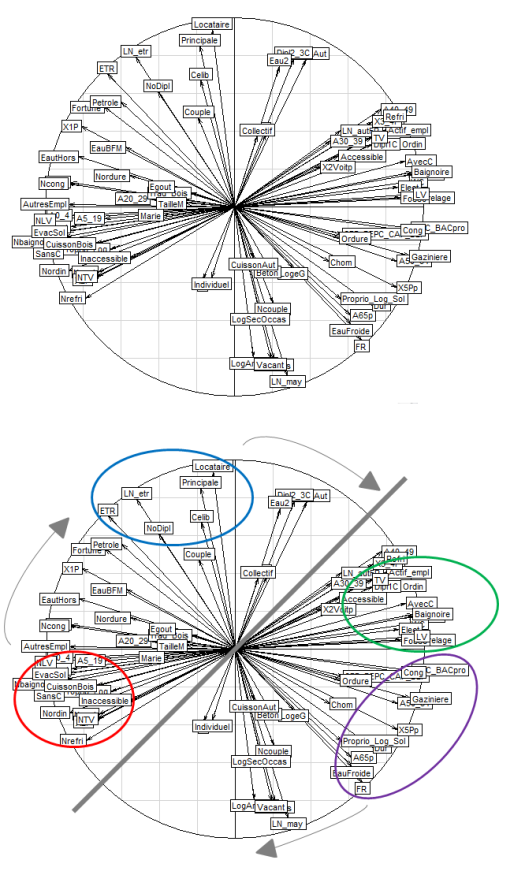
Quatre groupes principaux et trois groupes de transitions se dégagent. L’ACP permet d’ériger une carte caractéristique du type d’habitat, ainsi on a en rouge des logements précaires, en bleu ceux des étrangers, en vert des logement plus confortable et en violet les logements moins précaires.

– En rouge (s’oppose directement au groupe vert) : la population des 0-4 ans, les non scolarisés, les logements de 2 pièces, les ménages sans voiture, les logements sans confort, sans électricité, sans baignoire, sans ordinateur, sans téléviseur, sans réfrigérateur, sans lave-linge, inaccessible pour les voitures, les logements dont l’évacuation des eaux usées se fait par le sol, les ménages ayant recours à un mode de cuisson par bois.

– Le premier groupe de transition en gris, situé au dessus du groupe rouge: les ménages ayant recours aux réchauds à pétrole, les logements de fortune, les logements d’une pièce, les ménages sans eau à l’intérieur du logement et n’allant pas à la BFM s’approvisionner, les logements sans congélateur et les logements dont le sol est en terre battue.

– En bleu (s’oppose directement au groupe violet) : les locataires, les résidences principales, les nés à l’étranger, les célibataires (ou veufs ou divorcés), les étrangers et les sans diplôme.

– Le second groupe de transition en gris, situé à droite du groupe bleu : les logements ayant l’eau froide et l’eau chaude à l’intérieur du logement, les diplômés du second et troisième cycle et ceux dont le logement antérieur n’était pas en France.

– En vert (s’oppose directement au groupe rouge) : les logements équipés de réfrigérateur, les 40-49 ans, les logements de 3-4 pièces, ceux qui travaillent, les logements équipés de téléviseur, d’ordinateur, de baignoire, d’électricité, de lave-linge, de WC, les diplômés du premier cycle, les logements avec confort, les ménages ayant une voiture, les logements dont le sol est en carrelage et les logements dont l’évacuation des eaux usées se fait par fosse septique.

– En violet (s’oppose directement avec le groupe bleu) : les diplômés d’un BAC ou d’un BAC professionnel, les logements avec congélateur, gazinière, les 50 ans ou plus, les logements de 5 pièces ou plus, les propriétaires du logement et du sol, les habitations en dur, les logements avec uniquement l’eau froide à l’intérieur et les français.

– Et le troisième groupe de transition en gris, et situé en bas du groupe violet : les nés à Mayotte, les résidences vacantes, ceux dont le logement antérieur était à Mayotte et les étudiants.

On a donc une première typologie avec le groupe rouge représentant la population des très précaires. Ensuite le groupe bleu, qui est indépendant au groupe rouge et au groupe vert, se situe à côté des deux groupes gris de transition (gauche, précarité, et haut, développé) et qui s’inscrit finalement dans une classe intermédiaire. Puis le groupe vert qui, en opposition directe avec le groupe rouge, indique une population plus riche et qui reste très proche du groupe violet qui présente une forte corrélation en fonction de la tranche d’âge et du nombre de français. Puis le dernier groupe de transition, désignant la population des mahorais, étudiants, dont l’opposition se fait directement avec le groupe bleu des étrangers. A noter que les trois groupes de transition en gris sont indépendants les uns des autres, soit précarité, développé et jeunesse non liés.

On va boucler l’étude en focalisant sur la ressemblance entre les communes au travers de la caractérisation obtenue par l’ACP. La figure suivante présente, à droite, la projection des observations soit des communes,

Afin d’objectiver le regroupement des communes, une classification ascendante hiérarchique est réalisée,

Quatre profils de communes se dégagent :

– Pamandzi, Dzadouzi et Sada, dont les projections coïncident avec la typologie des zones développées ; 

– Boueni et Kani-Kéli, dont les projections coïncident avec l’autre typologie des zones développées; 

– Chiconi, Mtsangamouiji, Acoua et Mtsamboro dont les projections coïncident avec la typologie des jeunes ;

– Mamoudzou, Chirongui, Dandrélé, Tsingoni, dont les projections coïncident avec la typologie des étrangers et des zones précaires ;

– Bandraboua, Koungou, Dembeni et Ouangani, dont la projection coïncident avec la typologie des zones précaires.

Et l’on finalise tout cela par un résultat visuel et simple à lire. On rappelle que l’on est sur les données de 2012 :

Analyse spatiale de l’indice des prix

Parmi les nombreux jeux de données récupérables depuis le site de l’Insee, il en est un particulièrement intéressant : l’indice des prix à la consommation. On dispose ainsi d’une série chronologique allant de 1999 à 2017. N’étant pas expert sur le sujet, il semble que les données sont réajustées en fonction d’une année de référence, nommée base, faisant qu’il est difficile de travailler directement sur l’ensemble de toute la série. Néanmoins, le site de l’Insee permet d’avoir une série actualisée débutant à janvier 2012 et disponible depuis cette page web (cf données complémentaires) :

– Série de données : https://www.insee.fr/fr/statistiques?debut=0&theme=80&categorie=2&geo=DEP-976

A toute fin utile, on rajoutera la page définissant les données utilisées ici : https://www.insee.fr/fr/metadonnees/definition/c1557

• Approche descriptive

L’étude d’une telle série est l’occasion de se servir des outils d’analyse liés aux séries temporelles et aux chaînes de Markov. Mais avant cela, il est d’usage de décrire cette série de données au travers d’une analyse descriptive simple.

On a donc l’indice global des prix (bleu), celui lié à l’Alimentation (rouge), aux Services (orange), à l’Énergie (violet) et aux Produits Manufacturés (vert).

De manière général, l’indice des prix global a connu une forte hausse en 2012 qui se poursuit sur les cinq années suivantes mais de manière plus lente. Si l’on se réfère au graphe, les indices des prix de l’Alimentation et des Services augmentent depuis 2012, le premier nettement plus fortement que le second. A contrario, celui des Produits Manufacturés ne fait que chuter. Concernant celui des Énergies, il a connu une lente chute de 2012 à fin 2014 puis oscille jusqu’en mi-2017 pour finalement reprendre sa croissance en fin 2017. On s’attend à l’avenir à ce que l’indice des prix reprenne sa progression au vu des quatre autres courbes.

Si l’on raisonne en termes de taux de croissance mensuels, les éléments ci-dessous permettent une description plus précise du phénomène d’année en année :

A l’exception de l’année 2015 (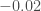), la croissance moyenne par mois est positive pour l’indice global des prix. Si elle reste relativement faible pour les années 2013 (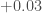), 2014 (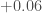), 2016 (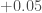) et 2017 (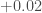), elle semble avoir connu un essor particulièrement important en 2012 (). Ce dernier constat est à relativiser étant donné la forte variabilité décrite par le calcul de l’écart-type, 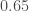en 2012 versus 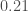(2017), 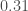(2013, 2016), 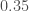(2015).

L’analyse des dotplots permet une caractérisation visuelle de la variabilité des taux de croissance mensuels pour chacune des sept années considérées :

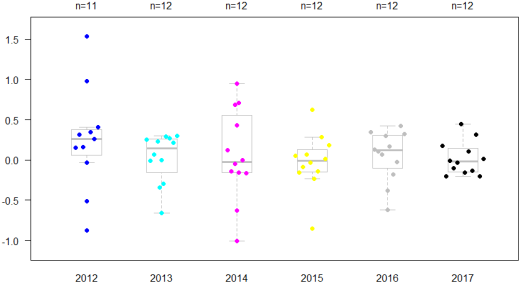
Cette approche met en évidence la grande variabilité évoquée des coefficients pour les années 2012 et 2014. Ce sont les années 2015 et 2017 qui, finalement, ont les plus faibles variabilités. Les années 2013 et 2016 montrant une tendance globale vers des taux de croissance mensuels négatifs à l’inverse de l’année 2017 dont la tendance est plutôt positive.

On peut également passer par une approche en trimestre en posant la période de janvier, février, mars ; 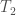la période d’avril, mai, juin ; celle de juillet, août, septembre et 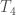pour octobre, novembre, décembre :

Il en ressort que les période avec les plus grandes variables sont le début de l’année () avec une tendance globale positive et le début du second semestre () nulle. 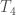étant particulièrement compact en termes de distribution tout comme .

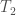• Approche par chaînes de Markov

On peut considérer une modélisation de l’indice des prix global par les chaînes de Markov. Via cette approche, il ne sera pas possible de dépasser l’ordre trois étant donné qu’au-delà le nombre de cas devient trop faible pour établir des trajectoires suffisamment robustes.

En codant 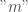le cas où le coefficient de variation est inférieur à 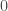et 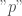celui où il est supérieur à 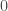, on obtient les trois tableaux de trajectoires suivants avec en ligne les états précédents de la chaîne et en colonne l’état actuel :

En prenant soin de considérer le rapport entre pourcentage de trajectoires et nombre de cas, on peut retenir les situations suivantes :

– pour l’ordre un, on a 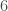chances sur 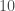d’observer un coefficient positif après un coefficient négatif (trajectoire : ).

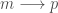– pour l’ordre deux,

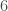on a chances sur 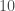d’observer un coefficient positif après deux coefficients négatifs (trajectoire: ) ;

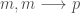on a 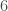chances sur 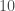d’observer un coefficient positif après un coefficient négatif suivi d’un coefficient positif (trajectoire : ) ;

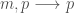on a 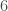chances sur 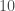d’observer un coefficient positif après un coefficient positif suivi d’un coefficient négatif (trajectoire : ).

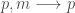– pour l’ordre trois,

on a chances sur 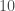d’observer un coefficient positif après trois coefficients négatifs (trajectoire: ) ;

on a chances sur 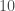d’observer un coefficient positif après deux coefficients négatifs suivis d’un coefficient positif (trajectoire: ) ;

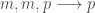on a 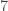chances sur 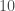d’observer un coefficient positif après deux coefficients positifs suivis d’un coefficient négatif (trajectoire: ) ;

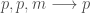on a 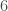chances sur 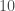d’observer un coefficient négatifs après trois coefficients positifs (trajectoire: ).

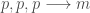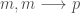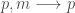Sur les huit cas que l’on a retenu, finalement deux sont inutiles ( et ) puisqu’ils présentent des probabilités similaires avec la trajectoire d’ordre un ).

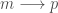En termes de prédiction, on est pour le mois de décembre 2017 sur un coefficient de variation positif mais on n’a pas pu déterminer de trajectoire suffisamment fiable pour rester sur l’ordre un. Si on se reporte à l’ordre deux, le mois de novembre 2017 est sur un coefficient de variation négatif ce qui renvoie au second cas de figure qui prédirait un coefficient positif en janvier 2018 dans 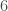cas sur 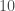. En jetant un œil à l’ordre trois, le mois d’octobre 2017 est également associé à un coefficient de variation négatif, ce qui prédit également un coefficient positif dans 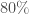des cas. En consultant les données de l’Insee, on conste cependant que l’indice passe de à 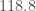, soit une baisse, venant contredire cette prédiction.

• Approche par série chronologique
  

L’échec de l’approche par chaîne de Markov est à modérer car les trajectoires retenues laissaient une grande part d’incertitude si l’on prend un peu de recul. On se propose cette fois-ci de passer par une tout autre approche, celle par série chronologique.

On a donc deux points à analyser avant de pouvoir se lancer dans les prédictions : la stationnarité et la saisonnalité. C’est deux points permettront de déterminer quel type de modèle l’on devra privilégier parmi les suivants : 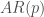, , 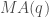, 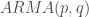ou .

L’étude des l’autocorrélogrammes est une étape importante dans l’analyse d’une série chronologique. Ci-dessous ceux obtenus sur les données :

On retrouve en haut à gauche la série de données d’origine et à sa droite l’autocorrélogramme. Ce dernier permet de tirer les cinq conclusions suivantes :

– Une décroissance lente des autocorrélations qui implique l’absence de stationnarité ;

– L’absence d’effet « sinusoïdale » des autocorrélations impliquant qu’il n’y a pas de saisonnalité ;

– L’aspect inversé qui dénote une inversion de tendance autour de la 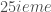observation (soit janvier 2014) et qui peut s’expliquer par une saisonnalité observable de 2012 à 2013, tous les six mois, mais qui disparait pour les années 2014 à 2017 ;

– Des autocorrélations qui, passées un retard de 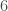, deviennent non significatives ;

– Les autocorrélogrammes partiels (figure en bas à gauche) et inversés (en bas à droite) aurait tendance à s’orienter vers les paramètres 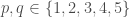étant donné que pour ces lags, pas ou retard les autocorrélations restent significatives.

Cette première analyse permet d’exclure l’usage du modèle SARIMA qui est applicable aux séries présentant une saisonnalité et le modèle ARMA, quant à lui applicable à celles stationnaires . On s’orientera donc vers un modèle ARIMA.

Pour le choix du modèle optimal et donc des paramètres 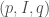on va se baser sur les tests statistiques de Dickey-Fuller augmenté. Il faudra générer un nombre de lags, pas ou retards et fouiller dans les résultats des tests celui qui rejette l’hypothèse 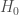de racine unitaire.

On va fixer un pas, lag ou retard de 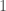à 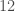(en lien avec le nombre de mois sur une année) et observer le comportement des tests au fur et à mesure que l’on augmente le degré de différentiation 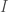du modèle (et dont l’objectif est de rendre stationnaire le processus afin d’optimiser les prédictions). On obtient dés lors le tableaux de résultats suivants (le test « trend » pour l’étude de la tendance et le test single mean pour l’étude de l’écart à la moyenne globale):

La condition pour retenir le meilleur modèle est le nombre de différentiation 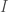qui ne rejette pas 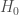pour les quatre tests ci-dessus. Plusieurs combinaisons ressortent, il convient alors de retenir la plus simple soit celle présentant le moins de lags, pas ou retards. C’est le cas qui nécessite 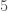dérivations qui semblent répondre au mieux aux critères. Maintenant que l’on a déterminer le paramètre 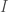, il nous reste à déterminer ceux optimisant 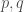. Pour cela on teste les différentes combinaisons possibles dans l’ensemble que l’on a défini grâce à l’analyse des autocorrélogrammes et retenir celui qui minimise le critère : 

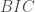C’est donc le modèle ARIMA(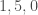) qui optimise la modélisation. Ce dernier étant établi, on passe maintenant aux prédictions. On génère alors le graphe suivant :

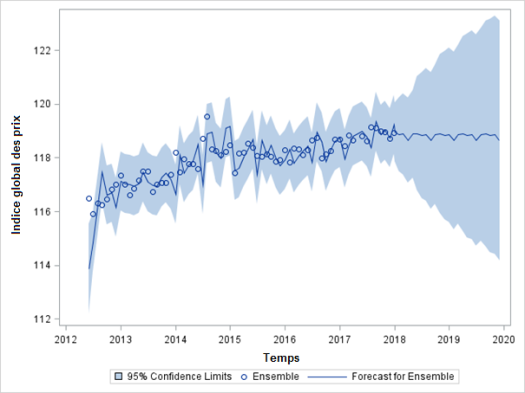
Pour l’année 2018, les prédictions envisagées de l’indice global des prix sont donc les suivantes :

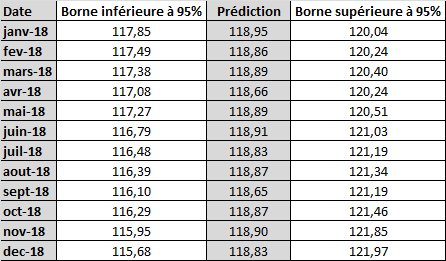
Si on compare avec les informations mises à disposition par l’Insee, il en ressort le constat suivant :

– Pour janvier, la valeur réelle de l’indice des prix global est de 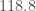, le modèle ayant prédit une valeur très proche () ;

– Pour février, la valeur réelle de l’indice des prix global est de , le modèle ayant prédit une valeur peu éloignée () ;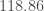

– Pour mars, l’Insee n’a pas publié la valeur, aucun comparatif n’est possible ;

– Pour avril, la valeur réelle de l’indice des prix global est de 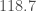, le modèle ayant prédit une valeur très proche () ;

En termes de tendance, le modèle avait prévu la chute de l’indice entre janvier et février (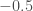 pour les valeurs réelles versus 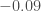pour les valeurs prédites) mais avait également prédit une nouvelle chute pour avril alors que dans les faits l’indice global des prix est remonté ( 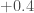pour les valeurs réelles versus pour les valeurs prédites).

• Approche par régression linéaire multiple

Afin de conclure l’analyse, on proposons d’étudier la relation entre l’indice des prix global et ceux associés à l’Alimentation, aux Produits Manufacturés, à l’Énergie et aux Services. L’idée étant d’observer l’influence de chacun de ces indices sur le global. 

Étant donné la nature des données qui sont de format continue, le modèle linéaire semble le plus approprié. Reste à définir si on reste sur une régression linéaire multiple ou si on opte pour sa version PLS. Afin d’argumenter ce futur choix, on regarde les matrices des corrélations de Pearson, Spearman et Kendall :

Les conclusions que l’on en tire à la lecture sont :

– Une forte corrélation linéaire entre les indices des prix de l’Alimentation et des Services avec l’indice global (respectivement 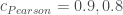). Ainsi, qu’une forte corrélation monotone décroissante avec les Produits Manufacturés (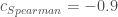). A contrario il n’y a pas de relation significative avec l’indice des prix associé à l’Énergie ().

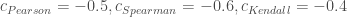– L’existence d’une forte multicolinéarité entre les indices des prix de l’Alimentation, des Produits Manufacturés, de l’Énergie et des services. Notamment la présence de deux groupes de variables avec, d’un côté, les indices associés à l’Alimentation et aux Services et, d’un autre côté, ceux de l’Énergie et des Produits Manufacturés.

Les corrélations et anti-corrélations sont particulièrement fortes, par conséquent on peut s’orienter vers un modèle linéaire PLS qui sera mieux adapté. La subtilité revient alors à déterminer le nombre de composantes PLS à retenir pour définir les coefficients de régression finaux. Pour cela, on  étudie les performances du modèle en fonction de la variance expliquée pour les quatre composantes calculables :

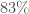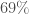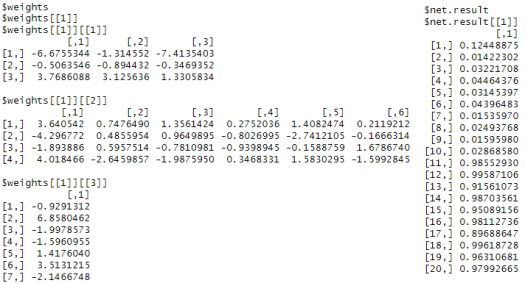
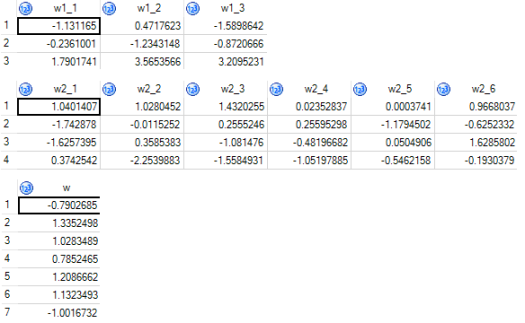
On constate que la première composante explique de la variance des quatre variables explicatives et avec la variable à expliquer (Indice des prix global). En poussant le nombre de composantes, on parvient à des résultats très bons pour trois composantes, pour les deux. Par conséquent, le choix de trois composantes peut être retenu, ce qui donne les coefficients de régression linéaire PLS suivants :

La sortie des coefficients permet de déterminer le poids des différents indices ainsi que leur influence sur l’indice des prix global. Ainsi, ce sont les indices liés à l’Alimentation et aux Produits Manufacturés qui pèsent le plus dans la croissance ou la décroissance de l’indice des prix global. Et si on se reporte aux coefficients standardisés, on en conclut que l’indice des prix de l’Alimentation a un impact 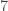fois plus important que celui de l’Énergie et 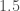fois plus important que celui des Services. Quant à celui des Produits Manufacturés, le rapport de force est de 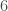fois plus important par rapport aux Énergies et fois plus important pour les Services. C’est donc le rapport de force entre Alimentation et Produits Manufacturés qui sera déterminant, sachant qu’il tourne en faveur du premier avec un coefficient de fois plus impactant que le second.

L’Analyse canonique des corrélations

Harold Hotelling

Historique :

Sommaire :

• Présentation
• L’Analyse canonique des corrélations
• Annexe théorique
• Exemple
• Application sous R
• Application sous SAS
• Bibliographie

Présentation :

L’Analyse canonique des corrélations, élaborée par Harold Hotelling en 1936, est une approche multivariée visant à comparer les interactions de deux matrices et continues. Les deux blocs peuvent être appariés ou non appariés, l’outil étant efficace dans les deux cas.

L’Analyse canonique des corrélations, comme son titre l’indique, se base sur les corrélations, autrement dit sur la présence ou l’absence d’une relation linéaire entre les variables des deux différents blocs.

L’outil appartient à la famille de l’analyse exploratoire et permet, par exemple, de comparer des champs thématiques d’information en élaborant une carte des variables et des observations permettant une représentation visuelle synthétique des interactions entre deux blocs de données.

L’analyse canonique des corrélations :

Hypothèse préliminaire : , continues.

L’Analyse canonique des corrélations se déroule en sept étapes,

– Étape 1 : Centrer-réduire les variables de et   (quoi que non obligatoire mais fortement recommandé).

– Étape 2 : Procéder à la décomposition de Gram-Schimdt () de et . On rappelle qu’une décomposition revient à écrire,

, où , matrices orthogonales et , matrices triangulaires supérieures. On utilisera ensuite la matrice , respectivement , dont le triangle supérieur contient , respectivement , et le reste de la matrice la forme compacte de , respectivement .

– Étape 3 : Extraire la matrice de , et de . Puis faire le produit,

– Étape 4 : Extraire du produit réalisé précédemment les valeurs propres , parts de variance expliquée, et les vecteurs propres associés et qui serviront à boucler les calculs.

– Étape 5 : Calculer les coefficients de corrélation canonique,

– Étape 6 : Calculer les axes factoriels, soit la projection des observations,

– Étape 7 : Projection des variables dans le plan factoriel,

Le choix du nombre d’axes se fait comme pour les autres méthodes d’analyse exploratoire, à partir des valeurs propres et en fonction de leur distribution. Etant donné que l’interprétation est menée analoguement à celle d’une Analyse en Composantes Principales (ACP), alors :

– Plus une variable de l’un des deux blocs est proche du cercle de corrélation et plus elle interagit avec les variables de l’autre bloc ;

– Plus les variables de différents blocs sont proches entre elles et plus leur corrélation est forte, soit que les variables de l’un des deux blocs peuvent s’écrire comme combinaison linéaire à partir des variables de l’autre bloc ;

– Un angle de ° entre deux blocs de variables implique une anti-corrélation entre eux ;

– Un angle de ° entre deux blocs de variables implique l’absence de corrélation entre eux.

Annexe théorique :

On présente ici une esquisse de la démarche méthodologique de l’analyse canonique des corrélations.

Soit muni de la métrique . L’idée est alors de chercher un couple de vecteurs normés sous contrainte d’obtenir l’angle le plus petit et ensuite le couple -orthogonal sous cette même contrainte. On en fait de même pour les autres couples .

Les opérateurs utilisés sont alors de la forme :

,

, dont l’une des propriétés les plus intéressantes est que la restriction de est diagonalisable, de valeurs propres -orthogonales et de vecteurs propres réels positifs.

Cette propriété se démontre facilement par le fait que,

, étant donné que sont -symétriques.

Dés lors, les vecteurs propres , -normés de sont associés aux mêmes valeurs propres. De plus, ils s’expriment comme combinaisons linéaires de et :

, ,

, avec facteurs canoniques obtenus par,

En passant par la formule des matrices de covariance, on en déduit que les équations des facteurs canoniques sont de la forme,

Exemple :

Soit les deux groupes de variables et suivants à comparer,

Dans un premier temps on va centrer-réduire les deux thèmes de variables. On notera alors les résultats : et . Puis on calcule leur décomposition :

On en récupère ensuite les parties orthogonales  : 

, dont le produit donne : 

Pour le calcul des valeurs propres et vecteurs propres associés utiles à la suite des calculs, on procède au développement en valeurs singulières du résultat obtenu précédemment,

, et,

Il va falloir les parties triangulaires pour la suite  : 

Maintenant, on va calculer les coefficients finaux par les deux produits matriciels suivant :  

Ensuite, les projections des observations relatives à et ,

, et,

On peut désormais calculer les coordonnées des variables de et de ,

, que l’on projette dans le plan en deux dimensions (choix motivé par simplicité de lecture étant donné qu’il s’agit d’un exemple),

– Les variables ne sont pas assez proches du cercle de corrélation pour être interprétées.

– Deux groupes sont à relever, le premier concerne les variables soit la possibilité de prédire à partir d’une combinaison linéaire des variables . Le second concerne les variables , soit un lien direct très fort entre elles.

– Les deux groupes décrits ci-dessus sont indépendants étant donné qu’ils forment un angle de °.

– Enfin, la variable est anti-corrélée (angle de °) au premier groupe décrit et indépendante au second (angle de °).

Application sous R :

Soit l’exemple suivant :

E = data.frame(X1 = c(0.8970, 2.0949, 3.0307, 4.0135, 5.0515, 6.0261, 6.9059, 7.9838, 8.9854, 9.9468), X2 = c(8.1472, 9.0579, 1.2699, 9.1338, 6.3236, 0.9754, 2.7850, 5.4688, 9.5751, 9.6489), X3 = c(3.1101, 4.1008, 4.7876, 7.0677, 6.0858, 4.9309, 4.0449, 3.0101, 5.9495, 6.8729), X4 = c(1.9593, 2.5472, 3.1386, 4.1493, 5.2575, 9.3500, 10.1966, 11.2511, 9.6160, 10.4733), X5 = c(11.1682, 11.9124, 12.9516, 13.9288, 14.8826, 15.9808, 16.9726, 18.1530, 18.9751, 19.8936), X6 = c(1.5761, 9.7059, 9.5717, 4.8538, 8.0028, 1.4189, 4.2176, 9.1574, 7.9221, 9.5949), X7 = c(1.0898, 1.9868, 2.9853, 10.0080, 8.9052, 8.0411, 2.0826, 1.0536, 9.0649, 10.0826), X8 = c(16.8407, 17.2543, 18.8143, 19.2435, 20.9293, 11.3517, 9.8308, 10.5853, 11.5497, 9.9172))

Package et fonction R : https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/cancor

La fonction cancor du package candisc permet de réaliser l’analyse canonique des corrélations. Après chargement de la librairie, on procède de la manière suivante :

cancor(x = E[,c(« X1 », « X2 », « X3 », « X4 »)], y = E[,c(« X5 », « X6 », « X7 », « X8 »)], xcenter = TRUE, xscale = TRUE, ycenter = TRUE, yscale = TRUE)

Parmi les éléments à insérer les plus importants il faut relever :

–  La première matrice de données thématiques : ;

–  La première matrice de données thématiques : ;

– Le fait de centrer-réduire le premier jeu de données : ;

– Le fait de centrer le second jeu de données : .

On obtient alors les résultats suivants :

, qui ne sont pas forcément les plus utiles, toutefois,

– On retrouve dans la colonne les valeurs propres, qui sont les mêmes que celles obtenues lors des calculs manuels (cf partie « Exemple ») ;

– L’application de la fonction sur l’objet créé permet d’afficher les coefficients canoniques, qui diffèrent de ceux obtenus par les calculs manuels (cf partie « Exemple ») non pas par l’algorithme utilisé mais par la façon de centrer-réduire les données ;

– Les coordonnées de projection des variables selon le plan voulu : , qui sont les mêmes que celles obtenues lors des calculs manuels (cf partie « Exemple »).

Application sous SAS :

Soit l’exemple suivant :

data E;
input Obs X1 X2 X4 X5 X6 X7 X8;
cards;
0.8970 8.1472 3.1101 1.9593 11.1682 1.5761 1.0898 16.8407
2.0949 9.0579 4.1008 2.5472 11.9124 9.7059 1.9868 17.2543
3.0307 1.2699 4.7876 3.1386 12.9516 9.5717 2.9853 18.8143
4.0135 9.1338 7.0677 4.1493 13.9288 4.8538 10.0080 19.2435
5.0515 6.3236 6.0858 5.2575 14.8826 8.0028 8.9052 20.9293
6.0261 0.9754 4.9309 9.3500 15.9808 1.4189 8.0411 11.3517
6.9059 2.7850 4.0449 10.1966 16.9726 4.2176 2.0826 9.8308
7.9838 5.4688 3.0101 11.2511 18.1530 9.1574 1.0536 10.5853
8.9854 9.5751 5.9495 9.6160 18.9751 7.9221 9.0649 11.5497
9.9468 9.6489 6.8729 10.4733 19.8936 9.5949 10.0826 9.9172
;
run;

Procédure SAS: https://support.sas.com/documentation/cdl/en/statug/63033/HTML/default/statug_cancorr_sect005.htm

La procédure CANCOR de SAS permet de réaliser l’analyse canonique des corrélations. On procède de la manière suivante :

proc cancorr data = E;
var X1 X2 X3 X4;
with X5 X6 X7 X8;
ods exclude MultStat StdCanCoefV StdCanCoefW;
run;

Parmi les éléments à insérer les plus importants il faut relever :

– La base de données où trouver les variables : ;

–  Les variables du premier thème : ;

–  Les variable du second thème : ;

– L’ODS exclude est utilisé pour supprimer les sorties sans intérêt.

On obtient alors les résultats suivants :

On vérifie,

– Le premier tableau (coupé en deux pour la mise en page) contient les valeurs propres, qui sont les mêmes que celles obtenues lors des calculs manuels (cf partie « Exemple ») ;

– Les deuxième et troisième tableaux (« Coefficients canoniques bruts. pour le/la Variables VAR/WITH ») contiennent les composantes et associée aux valeurs propres du premier tableau, qui diffèrent de celles obtenues lors des calculs manuels (cf partie « Exemple ») non pas par l’algorithme utilisé mais par la méthode pour centrer-réduire les données ;

– Les quatrième et cinquième tableaux (« Corrélation entre le(la) Variables VAR/WITH et leurs composantes canoniques ») contiennent les coordonnées des variables dans le plan factoriel, qui sont les mêmes que celles obtenues lors des calculs manuels (cf partie « Exemple »).

Bibliographie :

– Relations Between Two sets of Variates de Harold Hotelling ;

– Probabilités, analyse des données et Statistique de Gilbert Saporta ;

– Data mining et statistique décisionnelle. L’intelligence des données de Stéphane Tufféry ;

– Comprendre et utiliser les statistiques dans les sciences de la vie de Bruno Falissard ;

– Analyses factorielles simples et multiples de Brigitte Escofier et Jérôme Pagès ;

– La présentation powerpoint: http://iml.univ-mrs.fr/~reboul/canonique.pptx.pdf

La machine à vecteurs de support

Présentation:

La Machine à Vecteurs de Supports (SVM), également connue sous le nom de séparateurs à vaste marge, a été élaborée par Vladimir Vapnik en 1995. Elle est utilisée pour la classification d’une variable réponse binaire à partir d’une matrice de variables explicatives continues.

Les SVM s’appuient sur la notion de marge maximale et la notion de fonction noyau (kernel), permettant de traiter des problèmes de discrimination non-linéaire en reformulant le problème de classement comme un problème d’optimisation quadratique.

Les SVM font parties des techniques d’apprentissage supervisé et nécessitent le passage par une méthode de validation afin de généraliser leur résultat. En effet, il s’agit d’un outil très puissant permettant de modéliser avec une extrême précision un phénomène en fonction du noyau considéré, augmentant ainsi fortement le risque de surapprentissage.

Les machines à vecteurs de support:

Hypothèse préliminaire: binaire, continue.

L’Algorithme:

Le calcul des coefficients via les SVM est particulièrement coûteux étant donné qu’il se base sur la recherche d’une solution optimale au travers de noyau pouvant rallonger les ressources de calcul demandée, notamment pour le noyau polynomial. De plus, l’idée principale des SVM est d’estimer les vecteurs supports qui représentent les pondérations associées à chaque observation afin de déterminer leur influence sur l’élaboration de la frontière décisionnelle. En outre, plus il y a d’observations à considérer et plus le système associé à l’estimation de ces pondérations est important.

Quatre étapes sont à suivre pour estimer les coefficients , qui ne correspondent donc pas aux variables mais à nos individus pour lesquels l’influence est significative (ceux associés à un vecteur support négligeable sont alors supprimés du modèle prédictif final).

– Étape 0: Définir le noyau et les paramètres qui lui sont associés.

– Étape 1: Déterminer l’équation des vecteurs de support à partir des paramètres définis en étape 0,

– Étape 2: Déterminer la matrice à résoudre et dont la ème ligne est de la forme,

, où représente le vecteur des multiplicateurs de Lagrange.

– Étape 3: Rajouter à la matrice, conçue en étape 2, le vecteur en ligne et basé sur la contrainte de construction des . Ce système est alors noté .

– Étape 4: Résoudre le système via les multiplicateurs de Lagrange afin d’obtenir les estimations .

Équation prédictive:

L’Algorithme permet de déterminer les Lagrangiens soit les coefficients d’influence de nos vecteurs supports associés aux différentes observations. Cependant, les estimations ne sont pas suffisants pour la prédiction d’une nouvelle observation. Définissons l’ensemble des observations associées à un vecteur support non nul et dont l’influence doit être considérée pour la prédiction. L’Équation de prédiction est alors,

Où,

– est la notation utilisée pour désigner les valeurs caractéristiques associées aux variables explicatives considérées pour la nouvelle observation à prédire,

– le produit scalaire,

– le coefficient constant obtenu par,

, et dont la valeur ne varie pas quelque soit l’observation utilisée.

– les coefficients obtenus par,

Le choix du noyau:

Deux cas sont à distinguer lors de l’usage des SVM: le cas linéairement séparable et non linéairement séparable. Pour le premier, cela revient à construire une frontière linéaire optimale selon la notion de marge maximale. Le noyau est alors le noyau linéaire de formulation,

Pour le second cas, l’idée est de passer la construction d’une nouvelle dimension qui va envoyer les données dans un espace où la séparation est possible. Trois noyaux principaux existent parmi la longue liste disponible,

– le noyau polynomial ,

– le noyau radial , avec,

– le noyau sigmoïdale .

Où , et sont les paramètres à figer.

La sélection de variable:

Le choix des variables à retenir dans le modèle final amène à l’introduction du principe de « marge ». La marge correspond à la distance entre la frontière construite par le modèle et ses vecteurs supports. En général, un modèle est de bonne qualité si la marge est suffisamment éloignée des vecteurs supports, permettant ainsi plus d’aisance dans sa généralisation.

La sélection des variables se fait en fonction de la marge associée et notamment de sa sensibilité. L’Idée est de s’orienter vers un modèle dont la marge est la plus robuste possible.

La marge se calcul selon la formule suivante,

En définissant un facteur échelle qui est en fait le vecteur unitaire pondérant le noyau utilisé , le système à résoudre pour définir la sensibilité de la marge est alors,

Généralisation au cas multiclasse:

Les SVM ne sont pas directement transposables au cas multiclasse du fait d’une formule d’estimation basée sur un principe binaire. Pour se faire, l’idée est d’appliquer une approche du type « 1-contre-1 » et qui consiste, pour classes, à construire classifieurs et d’avoir recours à un schéma de vote afin de décider de la classe de prédiction.

Annexe théorique:

Nous présentons ici une esquisse de la démarche méthodologique conduisant à l’algorithme d’estimation des coefficients  d’un modèle basé sur les SVM.

Nous nous plaçons dans l’espace munit du produit scalaire. L’objectif est de construire une fonction qui sépare au mieux .

Le cas linéairement séparable:

Le plus simple, il s’écrit sous la forme suivante,

Avec,

– ,

– ,

La frontière de décision est un hyperplan, appelé hyperplan séparateur ou séparatrice. L’objectif est d’avoir,

Notion de marge maximale:

L’équation du séparateur linéaire montre que nous pouvons générer une infinité de classifieurs, la notion de marge prend alors toute son importance. Elle se définit comme étant la distance entre l’hyperplan et les observations les plus proches qui sont en fait nos vecteurs supports. L’hyperplan, à déterminer et qui maximise la marge, est donné par,

Formulation primale:

La distance de à l’hyperplan est donnée par sa projection orthogonale sur l’hyperplan,

La formule que nous recherchons se construit sous la contrainte:

Afin de faciliter l’optimisation, nous choisissons de normaliser et , de telle manière à ce que les observations à la marge ( pour les vecteurs supports sur la frontière positive, et pour ceux situés sur la frontière opposée) satisfassent,

–

–

La marge à maximiser vaut alors . La formulation dite primale des SVM est ainsi,

Minimiser sous contraintes que

Ceci peut se résoudre par la méthode classique des multiplicateurs de Lagrange , où le lagrangien est donné par,

Formulation duale:

Le lagrangien doit être minimisé par rapport à et , et maximisé par rapport à . Pour cela nous posons notre problème sous forme duale. Nous cherchons ainsi à annuler les dérivées partielles du lagrangien, selon les conditions de Kuhn-Tucker, Nous obtenons,

–

–

En réinjectant ces valeurs dans l’équation , nous avons la formulation duale suivante,

Maximiser

, sous les contraintes , et .

Ce qui nous donne les multiplicateurs de Lagrange optimaux . L’Equation de l’hyperplan solution devient alors,

Le cas non linéairement séparable:

Finalement l’hyperplan solution ne dépend que du produit scalaire entre et les vecteurs supports. Cette remarque est à l’origine de la deuxième innovation majeure des SVM: l’utilisation de la fonction noyau pour projeter dans un espace dit de redescription.

Plus formellement, nous appliquons aux vecteurs d’entrée , une transformation non-linéaire notée .

Dans cet espace, nous cherchons alors l’hyperplan,

, qui vérifie .

En utilisant la même procédure que dans le cas sans transformation, nous aboutissons au problème d’optimisation suivant,

Maximiser

, sous contraintes , et .

La fonction noyau:

Le problème de la formulation ci-dessus est qu’elle implique un produit scalaire entre vecteurs dans l’espace de redescription et de dimension élevée, ce qui est couteux en termes de calculs. Pour résoudre ce problème, nous utilisons une astuce connue sous le nom de « Kernel trick » consistant à utiliser une fonction noyau vérifiant,

D’où l’expression de l’hyperplan séparateur en fonction de la fonction noyau,

L’intérêt de la fonction noyau est double,

– le calcul se fait dans l’espace d’origine, ceci est beaucoup moins coûteux qu’un produit scalaire en grande dimension,

– la transformation n’a pas besoin d’être connue explicitement, seule la fonction noyau intervient dans les calculs, augmentant nettement les possibilités de discrimination.

Enfin, en accords avec le théorème de Mercer, doit être symétrique et semi-définie positive. L’approche par Kernel trick généralise ainsi l’approche linéaire.

Extension aux marges souples:

Cependant, il n’est pas non plus toujours possible de trouver une séparatrice linéaire dans l’espace de redescription. Il se peut aussi que des observations soient mal étiquetées et que l’hyperplan séparateur ne soit pas la meilleure solution au problème de classement.

Nous nous ramenons alors à la technique dite de marge souple, qui tolère les mauvais classements. La méthode cherche un hyperplan séparateur qui minimise le nombre d’erreurs grâce à l’introduction de variables ressorts , qui permettent de relâcher les contraintes sur les vecteurs d’apprentissage:

Avec les contraintes précédentes, le problème d’optimisation est modifié par un terme de pénalité qui agit directement sur les variables ressorts élevées et de formulation:

Minimiser

, où est une constante qui permet de contrôler le compromis entre nombre d’erreurs de classement et la largeur de la marge.

Exemple:

Soit le jeu de données suivant,

Certains le reconnaîtront, il s’agit de la fonction XOR également appelée fonction OU exclusif. Essayons de résoudre le problème en fonction des trois fonctions noyaux décrites pour le cas non linéairement séparable. La matrice de données qui lui est associée est la suivante,

Cas du noyau sigmoïdale:

Soit le noyau sigmoïdale de constante et de paramètre ,

Nous calculons pour chaque combinaison d’observations le valeur du noyau,

En rappelant la formule générale des ,

, nous obtenons la dérivation suivante,

Si nous raisonnons en termes de matrice afin de simplifier les calculs, cela revient à transposer les éléments de en fonction de . Nous obtenons alors la matrice,

Comme sous sommes sous contraintes que , nous rajoutons la condition au système à résoudre ainsi que la valeur de l’égalité (qui vaut car, pour respecter le passage des équations à la forme matricielle du problème, nous faisons pivoter le coefficient constant associé à la somme des à droite),

Nous résolvons ce système avec une régression linéaire et obtenons,

Tous nos coefficients sont différents de , nous en déduisons que pour ce noyau les quatre observations jouent un rôle de vecteur support.

Maintenant que les coefficients ont été estimés, nous pouvons déterminer la valeur de prédiction de . Nous calculons dans un premier temps les coefficients associés aux ,

Nous pouvons maintenant déterminer la prédiction de sur la base du modèle construit,

Cas du noyau radial:

Soit le noyau radial de paramètre ,

Nous calculons pour chaque combinaison d’observations le valeur du noyau,

En rappelant la formule générale des ,

, nous obtenons la dérivation suivante,

Si nous raisonnons en termes de matrice afin de simplifier les calculs, cela revient à transposer les éléments de en fonction de . Nous obtenons alors la matrice,

Comme sous sommes sous contraintes que , nous rajoutons la condition au système à résoudre ainsi que la valeur de l’égalité (qui vaut car, pour respecter le passage des équations à la forme matricielle du problème, nous faisons pivoter le coefficient constant associé à la somme des à droite),

Nous résolvons ce système avec une régression linéaire et obtenons,

Tous nos coefficients sont différents de , nous en déduisons que pour ce noyau les quatre observations jouent un rôle de vecteur support.

Maintenant que les coefficients ont été estimés, nous pouvons déterminer la valeur de prédiction de . Nous déterminons dans un premier temps les coefficients associé aux ,

Nous pouvons maintenant déterminer la prédiction de sur la base du modèle construit,

Cas du noyau polynomial:

Soit le noyau polynomial de degré , de constante et de paramètre ,

Nous calculons pour chaque combinaison d’observations le valeur du noyau,

En rappelant la formule générale des ,

, nous obtenons la dérivation suivante,

Si nous raisonnons en termes de matrice afin de simplifier les calculs, cela revient à transposer les éléments de en fonction de . Nous obtenons alors la matrice,

Comme sous sommes sous contraintes que , nous rajoutons la condition au système à résoudre ainsi que la valeur de l’égalité (qui vaut car, pour respecter le passage des équations à la forme matricielle du problème, nous faisons pivoter le coefficient constant associé à la somme des à droite),

Nous résolvons ce système avec une régression linéaire et obtenons,

Tous nos coefficients sont différents de , nous en déduisons que pour ce noyau les quatre observations jouent un rôle de vecteur support.

Maintenant que les coefficients ont été estimés, nous pouvons déterminer la valeur de prédiction de . Nous déterminons dans un premier temps les coefficients associé aux ,

Nous pouvons maintenant déterminer la prédiction de sur la base du modèle construit,

Application informatique:

Macro SAS:

%macro svm(DATA=,Y=,kernel=);

 /* Macro-programme pour le calcul des coefficients associés aux vecteurs supports.
       Les paramètres: – DATA, indique la base de données à traiter,
                       – Y, la variable réponse binaire ou multiclasse,
                       – kernel, le noyau (sigmoidale, radial, polynomial de degré 1-2-3-4).
       Sortie: la table coeffs_&kernel. des coefficients selon le noyau paramétré.

    /* Options nécessaires pour éviter de saturer le log et mettre en évidence les erreurs */
options nonotes spool;

   /* Sortie liste des variables explicatives */
proc contents data = &DATA. (drop =  &Y.) out = biblio noprint;
run;

    /* Listing variables explicatives et nombre */
proc sql noprint;
select distinct(name) into: list_vars separated by  »  » from biblio;
select count(*) into: nb_vars from biblio;
quit;

    /* Sortie effectif total */
proc sql noprint;
select count(*) into: nobs from &DATA.;
quit;

    /* Initialisation de la matrice des Y_i1 Y_i2 K(X_i1,X_i2) */
data Q;
run;

    /* Calcul par paire d’observations */
%do i1 = 1 %to &nobs.;

        /* Récupération 1ère observation */
data obs1;
set &DATA.;
if _n_ = &i1.;
rename &Y. = &Y.1;
%do p = 1 %to &nb_vars.;
rename %scan(&list_vars.,&p.) = %scan(&list_vars.,&p.)_1;
%end;
run;

%do i2 = 1 %to &nobs.;

            /* Récupération 2nde observation */
data obs2;
set &DATA.;
if _n_ = &i2.;
rename &Y. = &Y.2;
%do p = 1 %to &nb_vars.;
rename %scan(&list_vars.,&p.) = %scan(&list_vars.,&p.)_2;
%end;
run;

            /* Calcul de Y_i1 Y_i2 K(X_i1,X_i2) en fonction du noyau paramétré et de la paire d’observations considérées */
data pair;
merge obs1 obs2;
score = 0;
score1 = 0;
score2 = 0;
%do p = 1 %to &nb_vars.;
score = score + %scan(&list_vars.,&p.)_1*%scan(&list_vars.,&p.)_2;
score1 = score1 + %scan(&list_vars.,&p.)_1*%scan(&list_vars.,&p.)_1;
score2 = score2 + %scan(&list_vars.,&p.)_2*%scan(&list_vars.,&p.)_2;
%end;
%if &kernel. = sigmoidale %then %do;
score = &Y.1*&Y.2*tanh(1 + score);
%end;
%if &kernel. = radial %then %do;
score = &Y.1*&Y.2*exp(-sqrt((score1 + score2 – 2 * score)**2));
%end;
%if &kernel. = polynomial1 %then %do;
score = &Y.1*&Y.2*(1 + score);
%end;
%if &kernel. = polynomial2 %then %do;
score = &Y.1*&Y.2*(1 + score)**2;
%end;
%if &kernel. = polynomial3 %then %do;
score = &Y.1*&Y.2*(1 + score)**3;
%end;
%if &kernel. = polynomial4 %then %do;
score = &Y.1*&Y.2*(1 + score)**4;
%end;
run;

data Qadd;
set pair;
Obs1 = &i1.;
Obs2 = &i2.;
keep Obs1 Obs2 score;
run;

data Q;
set Q Qadd;
run;

%end;

%end;

    /* Finalisation de la liste des croisements et de leur score */
data Q;
set Q;
if Obs1 ne .;
score_deriv = – score;
run;

    /* Initialisation de la matrice des lagrangiens par la contrainte à respecter sum Y_i alpha_i = 0 */
proc transpose data = &DATA. (keep = &Y.) out = matsvm;
run;

data matsvm;
set matsvm;
score = 0;
drop _NAME_;
run;

    /* Pour chaque observation, on récupère la dérivée partielle pour le calcul des Lagrangiens */
%do i = 1 %to &nobs.;

data Qt;
set Q;
if Obs1 = &i.;
keep score_deriv;
run;

proc transpose data = Qt out = matsvm_add;
run;

data matsvm_add;
set matsvm_add;
score = -1;
drop _NAME_;
run;

data matsvm;
set matsvm matsvm_add;
run;

%end;

data matsvm;
set matsvm;
run;

    /* Sortie du dernier Lagrangien en guise de borne supérieur des Lagrangiens à considérer */
data _null_;
set &DATA.;
if _n_ = &nobs.;
lim_vars = compress(« COL »||_n_);
call symput (« lim_vars »,lim_vars);
run;

    /* Calcul des Lagrangiens par régression linéaire */
proc reg data = matsvm;
model score = COL1 — &lim_vars. / noint;
ods exclude NObs FitStatistics ParameterEstimates ANOVA;
ods output ParameterEstimates = coeffs;
run;

    /* Finalisation de la table des résultats finaux */
data Coeffs_&kernel.;
set coeffs;
Variable = tranwrd(Variable, »Alpha », »COL »);
Support = « N »;
if Estimate ne 0 then Support = « O »;
keep Variable Estimate Support;
run;

    /* Suppression des tables temporaires inutiles */
proc datasets lib = work nolist;
delete matsvm biblio Q Obs1 Obs2 pair Qadd Qt matsvm_add coeffs;
run;

    /* Reset des options */
options notes nospool;

%mend;

Package et fonction R: https://cran.r-project.org/web/packages/e1071/index.html

Bibliographie:

– The Elements of Statistical Learning de Trevor Hastie, Robert Tibshirani et Jerome Friedman.

– The Top Ten Algorithms in Data Minig de Xindong Wu et Vipin Kumar.

– Data Mining et statistique décisionnelle. L’intelligence des données de Stéphane Tufféry.

– Probabilité, analyse des données et statistique de Gilbert Saporta.

– SVM, Support Vector Machine. Machines à Vecteurs de Support – Séparateurs à Vaste Marge de Ricco Rakotomalala.

– Méthodes à noyaux – PART I de Alain Rakotomamonjy et Stéphane Canu.

– L’Article web: https://www.math.univ-toulouse.fr/~besse/Wikistat/pdf/st-m-app-svm.pdf

– Sélection de variables par SVM: application à la détection de piétons SVM Variable selection with application to pedestrian detection d’Alain Rakotomamonjy et de Frédéric Suard.

La méthode DISQUAL

Présentation:

La méthode DISQUAL, qui est l’acronyme de DIScrimination sur variables QUALitatives, a été élaboré par Gilbert Saporta en 1975. Elle permet de discriminer une variable polychotomique à classes à partir d’une matrice de variables qualitatives .

Le principe de base de la méthode DISQUAL est de combiner les bienfaits de l’Analyse des Correspondances Mulitples (ACM) avec celles de l’analyse discriminante linéaire ou quadratique de Fisher. Cette caractéristique fait de la méthode DISQUAL une sorte d’équivalent de la régression PLS (qui se base sur un mixte d’Analyse en Composantes Principales et de régression linéaire ou logistique), jouissant ainsi des mêmes propriétés bénéfiques qui sont: la possibilité de conserver plus de variables explicatives dans le modèle, des poids correctement réparties entre ces dernières et l’affranchissement des méfaits de la multicolinéarité.

Si la méthode DISQUAL est à réserver exclusivement à des variables qualitatives, une approche consistant à découper les variables continues en intervalles de valeurs pour les catégoriser est possible afin d’utiliser cet outil sur un format mixte de données.

DISQUAL:

Hypothèse préliminaire:  à classes et qualitative.

L’Algorithme associé à la méthode DISQUAL se déroule à cinq étapes qui sont les suivantes,

– Étape 1: Faire une ACM sur et en sortir les projections des variables sur l’ensemble des composantes ainsi que celles des observations .

– Étape 2: Former la matrice et sélectionner les axes non nuls et ainsi que ceux séparant au mieux les groupes de selon une analyse discriminante de Fisher linéaire ou quadratique sur les axes factorielles. Le critère utilisé en général est le de Wilks au seuil de puis en fonction du nombre d’axes retenus. Suite à ce premier filtre appliqué, devient , ensemble des axes factorielles retenus.

– Étape 3: Appliquer un second filtre sur  en retirant une par une les variables dont la p-valeur est la plus forte et en usant du critère de l'Aire (AUC), du volume (VUS) ou hypervolume (HUM) sous la Courbe ROC (AUC) en fonction du nombre de classe de obtenu selon une analyse discriminante de Fisher linéaire ou quadratique sur les axes factorielles. Nous supprimons ainsi les dimensions à partir desquelles ce critère chute. Suite à ce second filtre appliqué, devient

- Étape 4: Nous lançons une analyse discriminante de Fisher linéaire ou quadratique sur et obtenons ainsi les coefficients associés à chacune de nos composantes. Nous recherchons l'estimation combinée à partir de ces coefficients obtenus en soustrayant les coefficients par composantes en fonction des groupes de (dans le cas où est polychotomique, la distance euclidienne peut être une option).

- Étape 5: Le calcul des coefficients du modèle prédictif se fait alors en récupérant et en multipliant les coordonnées de nos modalités de variables par les coefficients respectifs à chacun de ces axes et obtenus en étape 4. La règle décisionnelle est alors de la forme suivante,

A noter que nous pouvons également fixer une étape de sélection des variables à cet algorithme lors de l'étape 1. Il faudrait alors lancer une première ACM sur , supprimer les variables dont l'ensemble des modalités ne sont que très peu contributives à la formation des axes et relancer une nouvelle ACM sur l'ensemble épuré de ces variables.

Annexe théorique:

Nous présentons dans cette partie de l'article une esquisse de la démarche méthodologique justifiant l'utilisation de la méthode DISQUAL.

La méthode DISQUAL se base sur un mélange d'ACM et d'analyse discriminante de Fisher. L'Utilisation d'une ACM sur un tableau de données qualitative revient à, dans un premier temps, transformer notre matrice en un tableau disjonctif complet, soit un tableau de indicatrices valant si l'observation a choisi tel modalité de tel variable et sinon.

Le problème de discrimination revient alors à lancer un analyse discriminante de Fisher sur ce tableau disjonctif et à estimer les coefficients propres à chaque modalité de chaque variable (ce qui revient à dire à chaque variable du dit-tableau). Nous pouvons alors reformuler l'objectif en la maximisation de la distance de Mahalanobis entre les centres de gravité des différents groupes de .

En ce sens, la méthode DISQUAL s’inspire donc très largement de la régression sur composantes principales (ou de la régression PLS) en lançant une analyse discriminante de Fisher sur nos axes factoriels.

Soit les composantes de l'ACM et les valeurs propres qui leur sont associés. L'Une des formidables propriétés des axes factoriels construis via une ACM est qu'ils sont orthogonaux, rendant l'inversion des matrices nécessaires au calcul possible comparé au cas où nous aurions directement travaillé sur le tableau disjonctif complet. Nous pouvons alors obtenir le score issue de la fonction de Fisher (dans le cas où binaire),

, avec,

L'Avantage de s'appuyer sur l'ACM est qu'il suffit d’effectuer la combinaison linéaire avec les mêmes coefficients des coordonnées de ses catégories. En effet, nous avons , où vecteur des coordonnées des modalités dans le plan factoriel. Nous avons alors,

Le score s'exprime alors comme la somme de la combinaison linéaire des indicatrices des modalités pour chaque individu. A noter que la règle décisionnelle ne comporte volontairement pas de terme constant.

Exemple:

Soit le jeu de données ci-dessous,

Appliquons la méthode DISQUAL, nous commençons donc par une ACM sur et sortons les coordonnées de nos individus sur les axes factoriels conçus,

Nous pouvons déjà filtrer six composantes sur les quinze attendues puisque nulles. Nous conservons donc .

Maintenant nous devons filtrer les dimensions à partir du modèle . Nous utilisons pour cela le test du de Wilks et obtenons les résultats suivants classés par ordre d'intégration selon une méthode descendante,

Au seuil de , sept axes sont significatifs. Par conséquent, nous les conservons tous à cette étape. Appliquons maintenant un second filtre basé sur l'AUC. Nous obtenons alors,

Il ressort du tableau ci-dessus que nous pouvons supprimer les dimensions puisque sur le modèle , l'AUC reste maximale.

Maintenant nous faisons tourner une nouvelle analyse discriminante de Fisher sur le modèle retenu et calculons le score en fonction des prédictions. Nous obtenons,

Nous avons maintenant nos coefficients par axe factoriel retenu. Place à l'estimation des coefficients de la règle décisionnelle en fonction des coordonnées des modalités de variables sur les axes ,

Application informatique:

Procédure SAS: http://od-datamining.com/download/#macro

Package et fonction R: http://finzi.psych.upenn.edu/library/DiscriMiner/html/disqual.html

Bibliographie:

- Probabilité, analyse des données et Statistique de Gilbert Saporta.

- Data Mining et statistique décisionnelle de Stéphane Tufféry.

Les méthodes de boosting

Yoav Freund (à gauche) et Robert Shapire (à droite)

Historique :

Sommaire :

• Présentation
• Le Boosting
  • Le concept général
  • L’algorithme AdaBoost
  • L’algorithme MARS
• Annexe théorique
• Exemple
• Application sous R
• Application sous SAS
• Bibliographie

Présentation :

Le Boosting est une famille d’outils d’analyse discriminante très puissants. L’idée est d’améliorer la règle de discrimination d’un classifieur sur plusieurs sous-parties de l’hyperplan formé par et d’établir la classification finale au travers d’un vote global pondéré. Chaque partie du plan se voit alors attribuer une pondération en fonction de sa performance de discrimination mise à jour itération par itération afin d’adapter la frontière décisionnelle en fonction des zones les plus difficiles à classer.

Le classifieur utilisé est la plupart du temps la régression linéaire, logistique ou les arbres de décision. Ils portent le nom de « classifieurs fiables » à la fois car ils sont simples d’utilisation mais également car l’objectif du Boosting est d’améliorer la règle de discrimination lorsqu’elle est peu performante.

Le Boosting appartient à la catégorie des méthodes d’apprentissage statistique nécessitant un jeu de d’apprentissage pour la conception de la règle d’apprentissage et un jeu de test pour sa validation afin de limiter les risques de sur-apprentissage. Comme la plupart d’entre elles, il a le principal défaut de concevoir une règle décisionnelle peu lisible d’où son surnom de boîte noire.

Parmi les méthodes de Boosting, la plus célèbre reste l’algorithme AdaBoost conçu par Yoav Freun et Robert Shapire en 1997 et définit pour la discrimination d’une variable réponse binaire à partir d’un ensemble de variables continues explicatives . D’autres algorithmes de Boosting sont également particulièrement répandus, on peut ainsi citer : l’algorithme Gentle Adaboost, Real Adaboost, MART et RankBoost.

Les algorithmes de Boosting :

Hypothèse préliminaire: binaire ou continue, continue.

Le concept général

Avant d’aborder les algorithmes Adaboost et MART, on présentera l’algorithme de Boosting de base.

– Étape initiale : Définir un classifieur faible , une fonction de coût , un nombre d’itérations d’entrainement pour l’optimisation des pondérations. On définit enfin les poids d’origine que l’on fixe à la même valeur quelque soit l’observation.

– Étapes itératives : Pour ,

• Étape 1 : On apprend le modèle, selon apprentissage statistique via tirage pondéré par les .
• Étape 2 : On applique le modèle construit, sur le sous-échantillon des observations qui n’ont pas été tirées à la première étape, aussi les ne sont pas réutilisés ici, et on récupère les prédictions obtenues : . Point important, si l’on ne souhaite pas utiliser d’apprentissage statistique alors ces deux premières étapes sont réalisées en même temps, on lance le classifieur faible directement en prenant en compte les .
  
• Étape 3 : On mesure le taux d’erreurs de classification de la règle décisionnelle conçue précédemment par la fonction de coût : .
• Étape 4 : On met à jour les pondérations , chaque observation mal classée se voit alors attribuer un poids plus important, ce qui donne .

– Étape finale : On détermine la règle décisionnelle finale par vote sur

L’algorithme AdaBoost

Pensé pour le cas où est binaire, AdaBoost utilisera l’arbre de décision comme classifieur faible. On n’évoquera pas l’utilisation de l’apprentissage statistique ici qui est le même que pour le concept général décrit ci-avant. L’Algorithme se décline de la manière suivante :

– Étape initiale : Initialisation des pondérations associées aux observations,

– Étapes itératives :

• Étape 1-2 : Détermination, selon apprentissage statistique, des prédictions en prenant en compte les poids ;
• Étape 3 : Calcul du taux d’erreurs : ;
• Étape 4 : Si alors le classifieur fait mieux qu’une règle aléatoire et on conserve le modèle, sinon on ajuste,
  • Le coefficient de pondération selon ses deux variantes :

La méthode de Breiman,

La méthode de Zhu pour le cas binaire,

• • Les pondérations :

– Étape finale : On obtient le modèle final,

L’Algorithme MART

L’Algorithme Multiple Additive Regression Trees se base sur l’utilisation d’arbres de régression. Par conséquent, il est adapté au cas où est continue. On n’évoquera pas l’utilisation de l’apprentissage statistique ici qui est le même que pour le concept général décrit ci-avant. Les différentes étapes d’estimation sont les suivantes :

– Étape initiale : Initialiser , avec fonction de perte à minimiser, et choix du nombre d’itérations .

– Étapes itératives : Pour ,

• Étape 1 : Pour calculer,

• Étape 2 : Estimer le modèle par arbre de régression sur et donnant les régions décisionnelles
• Étape 3 : Pour , calculer,

• Étape 4 : Mettre à jour

– Étape 2 : On a enfin la règle décisionnelle finale de forme

Annexe théorique :

Cette partie de l’article présente une esquisse de la justification de l’usage de la fonction de perte exponentielle.

L’algorithme AdaBoost se base sur l’idée nouvelle d’une fonction de perte exponentielle dont le principal avantage est computationnel. En partant du principe que , on montre facilement que,

Et équivalent à,

De cette manière, l’expansion additive produite par l’algorithme AdaBoost revient à estimer une partie du log-odds de . Ce qui justifie l’usage de son signe comme règle de classification décrite par la formule,

Un autre critère de minimisation de perte est la log-vraisemblance de la loi binomiale négative (appelée également déviance ou entropie croisée), interprétant comme une transformation logit. On a,

, avec . La fonction de perte est alors,

Et de déviance,

De la formule précédente, on voit que,

Exemple :

Soit l’échantillon suivant,

Ci-dessous le nuage de point basé sur ces données,

En vert la classe « A » et en rouge la classe « B »

On cherche donc à déterminer une fonction permettant de prédire les deux classes de en fonction des valeurs de . Comme il s’agit d’un exemple, on s’affranchira de la construction par apprentissage statistique.

On démarre en fixant les paramètres :

• Le classifieur faible sera l’arbre décisionnel, conformément au concept de l’AdaBoost, pour lequel on acceptera uniquement une profondeur d’un seul niveau ;
• L’échantillon complet servira de base d’apprentissage à chaque itération, comprendre que la règle produite le sera sur les observations ;
• On utilisera la méthode de Breiman pour le calcul du taux d’erreur ;
• On initialise tous les poids à pour chaque observation ;
• On choisit itérations pour la convergence du modèle.

Maintenant on peut lancer la procédure itérative . On obtient le modèle suivant :

, et de performance de classification :

Soit un taux de mauvaise classification pondérée de :

, lorsque prédiction pour l’observation ne correspond pas à la classe réelle, et lorsque c’est le cas.

Comme on utilise la méthode de Breiman, alors l’erreur corrigée vaut :

, que l’on propage ensuite pour rectifier le vecteur des pondérations , 

Enfin, on applique la dernière correction en divisant par :

, d’où,

On vient de boucler la première itération. On lance maintenant la seconde en reprenant alors les mêmes étapes. On obtient le même arbre de décision mais pour le cutoff : , ainsi que les mêmes performances. Soit un taux de mauvaise classification pondérée de :

On calcule ensuite l’erreur corrigée :

, que l’on propage ensuite pour rectifier le vecteur des pondérations , 

Enfin, on applique la dernière correction en divisant par :

, d’où :

On poursuit ainsi jusqu’à parcourir les autres itérations paramétrées, et en mettant à jour les pondérations. On obtient ainsi la matrice de classification à chaque itération suivante :

, et le vecteur des erreurs corrigées :

On procède au produit suivant afin de déterminer les scoring pour chaque observation : 

En attribuant la classe finale en fonction de la valeur la plus importante on obtient les performances décrites au travers de la matrice de confusion suivante :

, soit un taux de bonne classification globale de . Enfin, et plus concrètement, on peut afficher le découpage du plan comparé aux classes réelles.

Les bandes rouges correspondent à la région de la classe « A » construite par le modèle, en bleu celle de la classe « B ». En rouge les données réelles de la classe « A » et en vert celles de la classe « B »

Application sous R :

Soit l’exemple suivant :

E = data.frame(Y = c(rep(0,10),rep(1,10)),
X1 = c(8.1472, 9.0579, 1.2699, 9.1338, 6.3236, 0.9754, 2.7850, 5.4688, 9.5751, 9.6489, 1.5761, 9.7059, 9.5717, 4.8538, 8.0028, 1.4189, 4.2176, 9.1574, 7.9221, 9.5949),
X2 = c(3.1101, 4.1008, 4.7876, 7.0677, 6.0858, 4.9309, 4.0449, 3.0101, 5.9496, 6.8729, 1.0898, 1.9868, 2.9853, 10.0080, 8.9052, 8.0411, 2.0826, 1.0536, 9.0649, 10.0826))

Package et fonction R : 

La fonction boosting du package adabag permet d’appliquer l’algorithme AdaBoost. Après chargement du package, on lance sa conception de la manière suivante :

boosting(Y ~ X1+X2, data = E, boos = FALSE, mfinal = 10, coeflearn = « Breiman », control = rpart.control(minsplit = 7,minbucket=7))

Parmi les éléments à insérer les plus importants il faut relever :

– La formule définissant variable réponse (à gauche) et variables explicatives (à droite) : ~ ;

– La base de données sur laquelle on souhaite travailler : ;

– La non utilisation d’un échantillonnage à chaque itération : ;

– Le nombre d’itérations total : ;

– La correction de Breiman lors du calcul de l’erreur à chaque itération : ;

– Le paramétrage du classifieur faible qui sous R est obligatoirement l’arbre de décision : .

On obtient alors les résultats suivants :

On vérifie,

– Dans les sorties de type : , les différents arbres de décisions conçus à chaque itération (on a volontairement tronqué la sortie), et qui sont les mêmes que ceux obtenus lors des calculs manuls (cf partie « Exemple ») ;

– La somme des erreurs composants le vecteur à chaque itération : , qui sont les mêmes que celles obtenues lors des calculs manuls (cf partie « Exemple ») ;

– La valeur finale des votes par observation : (la sortie étant le résultat de chaque valeur divisé par la somme en ligne), qui sont les mêmes que ceux obtenus lors des calculs manuls (cf partie « Exemple ») ;

– Les classifications finales attribuées : , qui sont les mêmes que celles obtenues lors des calculs manuls (cf partie « Exemple ») ;

– Le poids d’influence des différentes variables du modèles : ;

– Les autres sorties indiquent le paramétrage de la fonction.

Application sous SAS :

Soit l’exemple suivant :

data BDD;
input x1 x2 Y;
cards;
8.1472 3.1101 A
9.0579 4.1008 A
1.2699 4.7876 A
9.1338 7.0677 A
6.3236 6.0858 A
0.9754 4.9309 A
2.7850 4.0449 A
5.4688 3.0101 A
9.5751 5.9495 A
9.6489 6.8729 A
1.5761 1.0898 B
9.7059 1.9868 B
9.5717 2.9853 B
4.8538 10.0080 B
8.0028 8.9052 B
1.4189 8.0411 B
4.2176 2.0826 B
9.1574 1.0536 B
7.9221 9.0649 B
9.5949 10.0826 B
;
run;

Il n’existe pas de procédure sous SAS permettant de lancer le Boosting. Par conséquent, on proposera la macro suivante :

%macro Boosting(DATA =, Y =, Classifieur =, FctCout = , Iteration = );

/* La macro ici présente permet d’appliquer l’algorithme AdaBoost en prenant pour classifieur faible la régression logistique.

Les paramètres utilisés sont :

– DATA, la base de données

– Y, la variable réponse binaire, par défaut toutes les autres variables seront utilisées pour la modélisation

– Classifieur, le type de classifieur faible, pour cette première version seule l’option LOG pour la régression logistique est disponible

– FctCout, la fonction erreur, pour cette première version seule celle de Breiman est disponible

– Iteration, le nombre d’itérations à utiliser pour le calcul des poids */

/* Options pour épurer la log */

options nonotes spool;

/* On rajoute 1 au paramètre ITERATION pour automatiser la classification finale en fait */

%let Itefin = %eval(&Iteration. + 1);

/* Récupération de la taille de l’échantillon */

proc sql noprint;

select count(*) into: n from &DATA.;

quit;

/* Récupération de la liste des variables autre que la réponse pour ériger le modèle */

proc contents data = &DATA. out = biblio noprint;

run;

proc sql noprint;

select distinct (name) into: list_var separated by  »  » from biblio where name ne « &Y. »;

quit;

data boosting;

set &DATA.;

/* Initialisation des pondérations */

P = 1/&n.;

run;

%do it = 1 %to &Itefin.;

/* Insérer ici un autre classifieur faible, il faut toutefois que le nouveau cas produise en sortie une table « out », incluant la classification obtenue */ 

%if &Classifieur. = LOG %then %do;

proc logistic data = boosting noprint;

model &Y. = &list_var.;

weight P;

output out = out predprobs = I;

run;

%end;

/* La dernière itération rajoutée est utilisée uniquement pour produire les prédictions sur les poids finaux */

%if &it. < &Iteration. %then %do;

/* Fusion des données d’origine et des prédictions pour arranger le calcul de l’erreur */

data boosting;

merge boosting out;

Y_hat = 0;

if &Y. = _into_ then Y_hat = 1;

err = P * Y_hat;

run;

/* Calcul de la correction */

proc sql noprint;

select sum(err) into: err from boosting;

quit;

/* Insérer ici d’autre fonction coût */

%if FctCout = Breiman %then %do;

%let err = %sysevalf(0.5 * log(1 – &err.)/&err.);

%end;

/* Propagation de la correction */

data boosting;

set boosting;

P = P * exp(P * Y_hat);

run;

/* Ajustement final des pondérations */

proc sql noprint;

select sum(P) into: err from boosting;

quit;

data boosting;

set boosting;

P = P/&err.;

keep P &Y. &list_var.;

run;

%end;

%end;

/* Production des performances en fin d’itération */

proc freq data = out;

tables _from_*_into_;

run;

/* Suppression des tables temporaires et inutiles */

proc datasets lib = work nolist;

delete biblio out;

run;

/* Reset des options d’affichage de la log */

options notes nospool;

%mend;

On applique la macro de la manière suivante :

%Boosting(DATA = E, Y = Y, Classifieur = LOG, FctCout = Breiman, Iteration = 200);

Parmi les éléments à insérer, il faut relever :

– Le tableau sur lequel on veut travailler : ;

– Le nom de la réponse à discriminer : ;

– Le type de classifieur même si un seul est disponible pour le moment (la régression logistique) : ;

– La fonction coût même si une seule est disponible pour le moment (celle de Breiman) : ;

– Le nombre d’itérations à réaliser : .

On obtient alors les résultats suivants parmi les tableaux générés en fin de procédure :

, et :

Le premier tableau présente les pondérations finales : , étant donné que l’on a privilégié sous SAS un classifieur différent de celui utilisé pour les calculs manuels, les résultats ne pourront être comparés.

Le second tableau présente les classifications finales, étant donné que l’on a privilégié sous SAS un classifieur différent de celui utilisé pour les calculs manuels, les résultats ne pourront être comparés. On remarquera alors que si l’on avait utilisé une simple régression logistique, les performances sont de de bonne classification, contre selon l’approche boosting.

Bibliographie :

– The Elements of Statistical Learning de Trevor Hastie, Robert Tibshirani et Jerome Friedman ;

– The top ten algorithms in data mining de Xindong Wu et Vipin Kumar ;

– Probabilité, analyse des données et Statistique de Gilbert Saporta ;

– Data mining et statistique décisionnelle. L’intelligence des données de Stéphane Tufféry.

Le modèle additif généralisé

Rob Tibshirani (à gauche) et Trevor Hastie (à droite)

Historique :

Sommaire :

• Présentation
• Le Modèle Additif Généralisé
  • L’algorithme Back-fitting
  • Les transformations
• Annexe théorique
• Exemple
• Application informatique
• Bibliographie

Présentation :

Le Modèle Additif Généralisé (GAM), élaboré par Trevor Hastie et Rob Tibshirani en 1990, est un outil permettant de discriminer une variable continue ou binaire à partir de variables explicatives continue transformées en amont. Dès lors, on chercher déterminer un jeu de fonction : travaillant chacune sur une variable unique ( mais aussi sur des combinaisons de deux ou plusieurs autres (). Le terme « Additif » vient du fait qu’il s’agira ensuite de sommer ces fonctions de transformation pour poser le modèle finale.

Le modèle GAM nécessite un jeu d’apprentissage pour sa construction et un jeu de test pour sa validation car il est sujet au sur-apprentissage du fait des fonctions de transformation utilisées particulièrement puissantes. En dépit de sa grande capacité avérée à modéliser tout type de phénomène, il reste peu conseillé lorsque l’on dispose d’un nombre de variables explicatives trop important du fait d’un coût de calcul très élevé.

Le Modèle Additif Généralisé :

Hypothèse préliminaire: continue, continue ou binaire.

La forme générale du modèle GAM est la suivante :

Avec , fonctions de transformation associée à la variable ou à un uplet de variables explicatives que l’on cherche à combiner directement.

L’Algorithme Back-fitting

Il s’agit de la méthode de calcul des coefficients de régression la plus couramment utilisée. L’algorithme Back-fitting, introduit par Jerome Harold Friedman et Werner Stuelzle en 1981, est une procédure itérative qui ajuste séquentiellement chaque composante lissée en maintenant les autres. Cette approche est similaire à l’algorithme de rétropropagation généralisée.

– Etape d’initialisation : poser , et

– Etape itérative : pour , déterminer,

• 
• 

Tant que,

décroît ou satisfait le critère de convergence

A noter que pour le terme,

Et pour le terme,

Enfin, l’estimation des différentes fonctions de lissage à l’instant , se fait selon la fonction lien retenue (modèle linéaire, logistique, etc).

Les transformations

Le modèle GAM se base donc sur la transformation de variables ou de combinaisons de variables afin bâtir son modèle prédictif. Elles portent le nom de fonctions de lissage et partagent toutes un concept bien particulier : celui d’ajustement par intervalle de valeurs appelé également « Nœud ». L’idée est d’optimiser le lissage partie par partie sans que les valeurs hors intervalles n’aient d’influence sur la zone focalisée. On peut définir ces nœuds soit arbitrairement soit en prenant les quantiles de distribution si l’on veut créer des intervalles de même longueur. Dans tous les cas on fixe le découpage suivant pour un nombre de nœuds :

d’indice de parcours

On aura à chaque fois autant de composantes de lissage, ou spline, que l’on fixera de nœuds. Une fois fait, on choisit parmi les principales fonctions de lissage suivantes pour la modélisation :

– La fonction Cubic Smoothing Spline de pénalité de courbure :

, avec et des coefficients constants à fixer au préalable. A noter que si .

– La fonction B-Splines à degrés du polynôme local et degrés de liberté :

, avec si , sinon.

– La fonction Thin-Plate Smooting Spline :

, avec , et coefficients de régression à paramétrer. A noter que si .

– La fonction P-Splines de force de pénalité , à degrés du polynôme local et degrés de liberté :

, où fonction B-splines déjà définie précédemment et coefficients à paramétrer. A noter que si l’on élève à nouveau l’intégrale au carré après calcul, on obtient la fonction Penalized Regression Splines.

– La fonction LOESS de noyau :

, où coefficients à paramétrer.

– La fonction de Base Radiale :

, où coefficients à fixer en amont, , paramètre de contrôle de la largeur de la fonction gaussienne.

– La fonction Tensor Splines de degrés du polynôme local et de degrés de liberté :

, où fonction B-splines déjà définie précédemment et coefficients à paramétrer.

Annexe théorique :

Cette partie de l’article présente une esquisse de la démonstration des fonctions Cubic Smoothing Spline, LOESS et Thin-Plate Smooting Spline à estimer pour déterminer les valeurs de selon la projection .

– On part de la formulation générique pour la fonction Cubic Smoothing Spline de paramètre :

Lorsque alors peut être n’importe quelle fonction d’interpolation de . Si , alors est la fonction des moindres carrés partiels et aucune derivée seconde ne peut être obtenue.

Pour obtenir une version simplifiée de la fonction Cubic Smoothing Spline, on pose un sous-ensemble de fonctions basiques et un vecteur de paramètres à estimer. La fonction d’origine peut alors se réécrire :

, avec et . La solution est alors,

, qui s’apparente à la régression ridge généralisée. Après développement, on obtient ainsi la forme simplifiée de ,

– On part de la formulation générique pour la fonction LOESS de noyau :

La fonction d’estimation est de la forme,

On définit alors la fonction du vecteur de valeurs , la matrice de régression de taille composée des et la matrice diagonale de taille et dont l’élément est . On a alors,

Ce qui donne une expression explicite pour l’estimation de la LOESS.

– On part de la formulation générique pour la fonction Thin-Plate Smooting Spline :

, avec et .

Soit et les fonctions de base de la forme des coordonnées de et de même pour la fonction . Nous définissons alors,

et

, que l’on peut généraliser avec la forme suivante,

Pour estimer cette fonction, l’idée est de résoudre le problème suivant,

, avec fonction de pénalisation visant à stabiliser .

De plus, si le paramètre alors la solution s’approche d’une fonction d’interpolation et si alors elle s’approche d’un plan des moindres carrés. Pour les valeurs intermédiaires de , la solution peut être représentée comme une fonction linéaire dont les coefficients sont obtenus par régression ridge.

La solution est alors de la forme,

, où et .

Exemple :

Soit l’échantillon suivant,

Ci-dessous le nuage de points basé sur ces données,

En vert la classe « A » et en rouge la classe « B »

On cherche donc à modéliser en fonction des valeurs de . Comme il s’agit d’un exemple, on s’affranchira de la construction par apprentissage statistique.

On applique sur une B-spline à degrés de liberté () et degré pour le polynôme local (). Pour commencer, on détermine arbitrairement le vecteur de nœuds, soit les paramétrés, selon un découpage homogène :

Pour chaque nœud, on calcule les valeurs de : , ce qui implique que l’on va devoir développer cinq composantes.

Pour la première composante :

, or par définition si , sinon. On a , .et .

, puisque et .

Ensuite, on calcul la seconde composante avec , et :

, puisque et .

Ensuite, on calcul la troisième composante avec , et :

, puisque et .

Puis, on calcul la quatrième composante avec , et :

, puisque et .

Et enfin, la cinquième composante : 

D’où,

On généralise la méthode de calcul à tous les éléments de et on obtient la matrice suivante :

On va maintenant appliquer la régression logistique de sur afin de déterminer les coefficients associés aux composantes B-spline de et à la forme non-transformée de .

On pourra alors consulter cette article qui détaille l’algorithme de calcul :  https://lemakistatheux.wordpress.com/category/outils-danalyse-supervisee/la-regression-logistique/

On obtient les résultats qui suivent :

Les performances obtenues peuvent être décrites au travers de la matrice de confusion suivante :

, soit un taux de bonne classification globale de . Enfin, et plus concrètement, on peut afficher le découpage du plan comparé aux classes réelles.

Les bandes rouges correspondent à la région de la classe « A » construite par le modèle, en bleu celle de la classe « B ». En rouge les données réelles de la classe « A » et en vert celles de la classe « B »

Application sous R :

Soit l’exemple suivant :

E = data.frame(Y = c(rep(0,10),rep(1,10)),
X1 = c(8.1472, 9.0579, 1.2699, 9.1338, 6.3236, 0.9754, 2.7850, 5.4688, 9.5751, 9.6489, 1.5761, 9.7059, 9.5717, 4.8538, 8.0028, 1.4189, 4.2176, 9.1574, 7.9221, 9.5949),
X2 = c(3.1101, 4.1008, 4.7876, 7.0677, 6.0858, 4.9309, 4.0449, 3.0101, 5.9496, 6.8729, 1.0898, 1.9868, 2.9853, 10.0080, 8.9052, 8.0411, 2.0826, 1.0536, 9.0649, 10.0826))

Package et fonction R: https://stat.ethz.ch/R-manual/R-devel/library/mgcv/html/gam.html

La fonction gam du package mgcv permet de réaliser des modèles additifs généralisés. Après chargement du package, on lance la construction du modèle de la manière suivante :

model = gam(Y ~ bs(X1, df = 5, degree = 1) + X2, data = E, family = binomial(link = « logit »))

summary(model)

Parmi les éléments à insérer les plus importants il faut relever :

–  La formule définissant variable réponse (à gauche) et variables explicatives (à droite) : ~ , on remarquera que cette dernière contient directement l’application de la fonction de lissage (ici une B-spline) sur tandis que pour on prendra sa forme d’origine. Enfin, à noter que doit être codée ;

– La base de données sur laquelle on souhaite travailler : ; 

– La fonction lien : ;

– La production de tous les détails du modèle construit : .

On obtient alors les résultats suivants :

On vérifie :

– La fonction lien : « Family : binomial », « Link function: logit » ;

– Le modèle paramétré : « Y ~ bs(X1, df = 5, degree = 1) + X2 » ;

– Les coefficients associés aux dérivations de et à dans la première colonne , qui sont les mêmes que ceux obtenus lors des calculs manuels (cf section « Exemple ») ;

– Le niveau de significativité de chaque coefficient dans la dernière colonne : « Pr(>|Z|) » ;

– Et les performances du modèle sur les deux dernières lignes.

Application sous SAS :

Soit l’exemple suivant :

data E;
input x1 x2 Y $1.;
cards;
8.1472 3.1101 A
9.0579 4.1008 A
1.2699 4.7876 A
9.1338 7.0677 A
6.3236 6.0858 A
0.9754 4.9309 A
2.7850 4.0449 A
5.4688 3.0101 A
9.5751 5.9495 A
9.6489 6.8729 A
1.5761 1.0898 B
9.7059 1.9868 B
9.5717 2.9853 B
4.8538 10.0080 B
8.0028 8.9052 B
1.4189 8.0411 B
4.2176 2.0826 B
9.1574 1.0536 B
7.9221 9.0649 B
9.5949 10.0826 B
;
run;

Procédure SAS: https://support.sas.com/documentation/cdl/en/statug/63033/HTML/default/viewer.htm#statug_gam_sect004.htm

La procédure GAM permet de réaliser des modèles additifs généralisés, toutefois elle n’offre pas un choix aussi varié que sous R. On lance la construction du modèle de la manière suivante :

proc gam data = E;
model Y (event = « B ») = spline(X1,df = 5) param(X2) / link = binomial;
ods exclude ConvergenceStatus InputSummary IterSummary ResponseProfile;
run;

Parmi les éléments à insérer les plus importants il faut relever :

–  La base de données sur laquelle on souhaite travailler : ; 

–  La formule définissant variable réponse (à gauche) et variables explicatives (à droite) : , on remarquera que cette dernière contient directement l’application de la fonction de lissage (ici une spline) sur tandis que pour on prendra sa forme d’origine ;

– La fonction lien : ;

– L’ODS output est utilisé afin de ne filtrer que les résultats d’intérêt.

On obtient alors les résultats suivants :

On vérifie :

– Dans le premier tableau, la liste des coefficients associés à chaque variable brute du modèle et , le manque de possibilité comparé à R fait que l’on aura appliqué ici un paramétrage différent non comparable à celui des calculs manuels ;

– Dans le deuxième tableau, le coefficient associé à la transformation de , le manque de possibilité comparé à R fait que l’on aura appliqué ici un paramétrage différent non comparable à celui des calculs manuels ;

– Dans le troisième tableau, les indicateurs de performance de la version transformée de .

Bibliographie :

– The Elements of Statistical Learning de Trevor Hastie, Robert Tibshirani et Jerome Friedman ;

– Data Mining et statistique décisionnelle. L’Intelligence des données de Stéphane Tufféry.