GAM – lemakistatheux

Rob Tibshirani (à gauche) et Trevor Hastie (à droite)

$\bullet$ Historique :

$\begin{tabular}{|l|c|c|} \hline Bloc & 07/12/2016-V1 & 16/02/2024-V2 \\ \hline Historique & & Cr\'eation \\ \hline Sommaire & & Cr\'eation \\ \hline Pr\'esentation & Cr\'eation & \\ \hline Le Mod\`ele Additif G\'en\'eralis\'e & Cr\'eation & Ajout de nouvelles fonctions \\ \hline Annexe th\'eorique & Cr\'eation & \\ \hline Exemple & & Cr\'eation \\ \hline Appli... Info... & Cr\'eation & Devient Appli... sous R \\ \hline Appli... sous SAS & & Cr\'eation \\ \hline Bibliographie & Cr\'eation & MAJ \\ \hline \end{tabular}$

$\bullet$ Sommaire :

Présentation
Le Modèle Additif Généralisé
- L’algorithme Back-fitting
- Les transformations
Annexe théorique
Exemple
Application informatique
Bibliographie

$\bullet$ Présentation :

Le Modèle Additif Généralisé (GAM), élaboré par Trevor Hastie et Rob Tibshirani en 1990, est un outil permettant de discriminer une variable $Y$ continue ou binaire à partir de $P$ variables explicatives continue $\mathbf{X} = (X ^1, \cdots, X^P)$ transformées en amont. Dès lors, on chercher déterminer un jeu de fonction : $f_1, \cdots, f_K$ travaillant chacune sur une variable unique ( $f_k (X ^p)$ mais aussi sur des combinaisons de deux ou plusieurs autres ( $f_k (X ^{p_1}, X ^{p_2}, \cdots)$ ). Le terme « Additif » vient du fait qu’il s’agira ensuite de sommer ces fonctions de transformation pour poser le modèle finale.

Le modèle GAM nécessite un jeu d’apprentissage pour sa construction et un jeu de test pour sa validation car il est sujet au sur-apprentissage du fait des fonctions de transformation utilisées particulièrement puissantes. En dépit de sa grande capacité avérée à modéliser tout type de phénomène, il reste peu conseillé lorsque l’on dispose d’un nombre $P$ de variables explicatives trop important du fait d’un coût de calcul très élevé.

$\bullet$ Le Modèle Additif Généralisé :

Hypothèse préliminaire: $\mathbf{X}$ continue, $Y$ continue ou binaire.

La forme générale du modèle GAM est la suivante :

$E[Y | X ^1, \dots, X ^P] = \alpha + \sum_{p = 1} ^P f_p (X ^p) + \sum_{k = 1} ^K f_k (X ^{p_1}, \cdots)$

Avec $f_p, f_k$ , fonctions de transformation associée à la variable $X ^p$ ou à un uplet de variables explicatives $(X ^{p_1}, X ^{p_2} \cdots)$ que l’on cherche à combiner directement.

L’Algorithme Back-fitting

Il s’agit de la méthode de calcul des coefficients de régression la plus couramment utilisée. L’algorithme Back-fitting, introduit par Jerome Harold Friedman et Werner Stuelzle en 1981, est une procédure itérative qui ajuste séquentiellement chaque composante lissée en maintenant les autres. Cette approche est similaire à l’algorithme de rétropropagation généralisée.

– Etape d’initialisation : poser $f_0 = E[Y] = \frac{1}{n} \sum_{i = 1} ^n Y_i$ , et $f_p ^0 = 0, \forall p \in[1, P]$

– Etape itérative $t$ : pour $p \in [1,P]$ , déterminer,

$R_p = Y - f_0 - \sum_{k = 1} ^{p - 1} f_k ^t (X ^k) - \sum_{k = p + 1} ^P f_k ^{t - 1} (X ^k)$
$f_p ^t = E[R_p | X ^p]$

Tant que,

$\frac{1}{n} || Y - f_0 - \sum_{p = 1} ^P f_p ^t (X ^p) || ^2$ décroît ou satisfait le critère de convergence

A noter que pour $p = 1$ le terme,

$\sum_{k = 1} ^{p - 1} f_k ^t (X ^k) = 0$

Et pour $p = P$ le terme,

$\sum_{k = p + 1} ^P f_k ^t (X ^k) = 0$

Enfin, l’estimation des différentes fonctions de lissage à l’instant $t, f_p ^t$ , se fait selon la fonction lien retenue (modèle linéaire, logistique, etc).

Les transformations

Le modèle GAM se base donc sur la transformation de variables ou de combinaisons de variables afin bâtir son modèle prédictif. Elles portent le nom de fonctions de lissage et partagent toutes un concept bien particulier : celui d’ajustement par intervalle de valeurs appelé également « Nœud ». L’idée est d’optimiser le lissage partie par partie sans que les valeurs hors intervalles n’aient d’influence sur la zone focalisée. On peut définir ces nœuds soit arbitrairement soit en prenant les quantiles de distribution si l’on veut créer des intervalles de même longueur. Dans tous les cas on fixe le découpage suivant pour un nombre $Q$ de nœuds :

$t_1 < t_2 < t_3 < \cdots < t_Q$ d’indice de parcours $q$

On aura à chaque fois autant de composantes de lissage, ou spline, que l’on fixera de nœuds. Une fois fait, on choisit parmi les principales fonctions de lissage suivantes pour la modélisation :

– La fonction Cubic Smoothing Spline de pénalité de courbure $\lambda \geq 0$ :

$CSS_q(X) = \sum_{i = 1} ^n [Y_i - g_q (X_i)] ^2 + \lambda \int_{[t_q, t_{q+1}]} (g_q '' (x)) ^2 dx$

, avec $g_q (X) = a_q + b_q \cdot (X - t_q) + c_q \cdot (X - t_q) ^2 + d_q \cdot (X - t_q) ^3$ et $a_q, b_q, c_q, d_q$ des coefficients constants à fixer au préalable. A noter que $g_q (X_i) = 0$ si $X_i \not in ]t_q, t_{q+1}[$ .

– La fonction B-Splines à $d \geq 1$ degrés du polynôme local et $K \geq 1$ degrés de liberté :

$\forall k \in [1, K], B_{k,d} (X) = \frac{(X - t_k)}{(t_{k + d} - t_{k})} \cdot B_{k, d-1} (X) + \frac{t_{k+d+1} - X}{t_{k+d+1} - t_{k+1}} \cdot B_{k+1,d-1} (X)$

, avec $B_{k,0} (X_i) = 1$ si $t_k \leq X_i < t_{k + 1}$ , $0$ sinon.

– La fonction Thin-Plate Smooting Spline :

$f(X) = \beta_0 + \beta \cdot X + \sum_{q = 1} ^Q \alpha_q \cdot g_q (X)$

, avec $g_q (x) = \theta(|| X - t_q ||)$ , $\theta(z) = z ^2 \cdot log z ^2$ et $\alpha, \beta$ coefficients de régression à paramétrer. A noter que $g_q (X_i) = 0$ si $X_i \not in ]t_q, t_{q+1}[$ .

– La fonction P-Splines de force de pénalité $\lambda \geq 0$ , à $d \geq 1$ degrés du polynôme local et $K \geq 1$ degrés de liberté :

$f(x) = \sum_{k=1} ^K \beta_k \cdot B_{k,d} (X) + \lambda \int [f''(X)]^2 dx$

, où $B_{k,d} (X)$ fonction B-splines déjà définie précédemment et $\beta$ coefficients à paramétrer. A noter que si l’on élève à nouveau l’intégrale au carré après calcul, on obtient la fonction Penalized Regression Splines.

– La fonction LOESS de noyau $K(.,.)$ :

$LOESS(X) = min_{\alpha(x_0), \beta(x_0)} \sum_{i = 1} ^n K (x_0, X_i) \cdot [Y_i - \alpha(x_0) - \beta(x_0) \cdot X_i] ^2$

, où $(\alpha, \beta)$ coefficients à paramétrer.

– La fonction de Base Radiale :

$RBF(X) = \sum_{q = 1} ^Q \beta_q \cdot \phi(|| X - t_q ||)$

, où $\beta$ coefficients à fixer en amont, $\phi(x) = e ^{- \frac{x ^2}{2 \sigma ^2}}$ , $sigma$ paramètre de contrôle de la largeur de la fonction gaussienne.

– La fonction Tensor Splines de $d \geq 1$ degrés du polynôme local et de $K_1, \cdots K_P \geq 1$ degrés de liberté :

$f(X ^1, X ^2, \cdots, X ^P) = \sum_{k_1 = 1} ^{K_1} \sum_{k_2 = 1} ^{K_2} \cdots \sum_{k_P = 1} ^{K_P} \beta_{k_1, k_2, \cdots, k_P} \cdot B_{k_1, d}(X ^1) \cdot B_{k_2, d}(X ^2) \cdot \cdots \cdot B_{l_P, d}(X ^P)$

, où $B_{k,d} (X)$ fonction B-splines déjà définie précédemment et $\beta$ coefficients à paramétrer.

$\bullet$ Annexe théorique :

Cette partie de l’article présente une esquisse de la démonstration des fonctions Cubic Smoothing Spline, LOESS et Thin-Plate Smooting Spline à estimer pour déterminer les valeurs de $\mathbf{X}$ selon la projection $f = (f_1, f_2, \cdots)$ .

– On part de la formulation générique pour la fonction Cubic Smoothing Spline de paramètre $\lambda \in [0, + \infty[$ :

$RSS(f,\lambda) = \sum_{i = 1} ^n [y_i - f(x_i)] ^2 + \lambda \int (f '' (t)) ^2 dt$

Lorsque $\lambda = 0$ alors $f$ peut être n’importe quelle fonction d’interpolation de $X$ . Si $\lambda = \infty$ , alors $f$ est la fonction des moindres carrés partiels et aucune derivée seconde ne peut être obtenue.

Pour obtenir une version simplifiée de la fonction Cubic Smoothing Spline, on pose $D_j(x)$ un sous-ensemble de $D$ fonctions basiques et $\theta$ un vecteur de paramètres à estimer. La fonction d’origine peut alors se réécrire :

$RSS(\theta,\lambda) = (y - D \theta) ^t (y - D \theta) + \lambda \theta ^t \Omega_N \theta$

, avec $\lbrace D \rbrace_{i,j} = D_j (x_i)$ et $\lbrace \Omega_N \rbrace_{j,k} = \int D_j '' (t) D_k '' (t) dt$ . La solution est alors,

$\hat{\theta} = (D ^t D + \lambda \Omega_D) ^{-1} D ^t y$

, qui s’apparente à la régression ridge généralisée. Après développement, on obtient ainsi la forme simplifiée de $f$ ,

$\hat{f}(x) = \sum_{j = 1} ^D D_j (x) \hat{\theta}_j$

– On part de la formulation générique pour la fonction LOESS de noyau $K$ :

$min_{\alpha(x_0), \beta(x_0)} \sum_{i = 1} ^n K_{\lambda} (x_0,x_i) [y_i - \alpha(x_0) - \beta(x_0) x_i] ^2$

La fonction d’estimation est de la forme,

$\hat{f} (x_0) = \hat{\alpha} (x_0) + \hat{\beta} (x_0) x_0$

On définit alors la fonction du vecteur de valeurs $b(x) ^t = (1,x)$ , $\mathbf{B}$ la matrice de régression de taille $N \times 2$ composée des $b(x_i) ^t$ et $\mathbf{W}(x_0)$ la matrice diagonale de taille $N \times N$ et dont l’élément $i$ est $K_{\lambda} (x_0, x_i)$ . On a alors,

$\hat{f} (x_0) = b(x_0) ^t \mathbf{B} ^t \mathbf{W} (x_0) \mathbf{B} ^{-1} \mathbf{B} ^t \mathbf{W} (x_0) y = \sum_{i = 1} ^N K_{\lambda} (x_0,x_i) y_i$

Ce qui donne une expression explicite pour l’estimation de la LOESS.

– On part de la formulation générique pour la fonction Thin-Plate Smooting Spline :

$f(x) = \beta_0 + \beta ^t x + \sum_{i = 1} ^n \alpha_i h_i (x)$

, avec $h_i (x) = \theta(|| x - x_p||)$ et $\theta(z) = z ^2 log z ^2$ .

Soit $\mathbf{X} \in \mathbb{R} ^2$ et les fonctions de base de la forme $h_{1,k} (X ^1), \forall k \in 1, \cdots, M_1$ des coordonnées de $X ^1$ et de même pour la fonction $h_{2,k} (X ^2), \forall 1, \cdots, M_2$ . Nous définissons alors,

$g_{j,k} (\mathbf{X}) = h_{1,j} (X ^1) h_{2,k} (X ^2), j = 1, \cdots, M_1$ et $k = 1, \cdots, M_2$

, que l’on peut généraliser avec la forme suivante,

$g(\mathbf{X}) = \sum_{j = 1} ^{M_1} \sum_{k = 1} ^{M_2} \theta_{j,k} g_{j,k} (\mathbf{X})$

Pour estimer cette fonction, l’idée est de résoudre le problème suivant,

$min_J \sum_{i = 1} ^N \lbrace y_i - f(x_i) \rbrace ^2 + \lambda J[f]$

, avec $J$ fonction de pénalisation visant à stabiliser $f$ .

De plus, si le paramètre $\lambda \rightarrow 0$ alors la solution s’approche d’une fonction d’interpolation et si $\lambda \rightarrow \infty$ alors elle s’approche d’un plan des moindres carrés. Pour les valeurs intermédiaires de $\lambda$ , la solution peut être représentée comme une fonction linéaire dont les coefficients sont obtenus par régression ridge.

La solution est alors de la forme,

$f(x) = \beta_0 + \beta^t x + \sum_{j = 1} ^N \alpha_j h_j (x)$

, où $h_j(x) = \eta(||x - x_j||)$ et $\eta(z) = z ^2 log z ^2$ .

$\bullet$ Exemple :

Soit l’échantillon $(Y, X ^1, X ^2)$ suivant,

$\begin{tabular}{|c|c|c|} \hline Y & X1 & X2 \\ \hline A & 8.1472 & 3.1101 \\ \hline A & 9.0579 & 4.1008 \\ \hline A & 1.2699 & 4.7876 \\ \hline A & 9.1338 & 7.0677 \\ \hline A & 6.3236 & 6.0858 \\ \hline A & 0.9754 & 4.9309 \\ \hline A & 2.7850 & 4.0449 \\ \hline A & 5.4688 & 3.0101 \\ \hline A & 9.5751 & 5.9496 \\ \hline A & 9.6489 & 6.8729 \\ \hline B & 1.5761 & 1.0898 \\ \hline B & 9.7059 & 1.9868 \\ \hline B & 9.5717 & 2.9853 \\ \hline B & 4.8538 & 10.0080 \\ \hline B & 8.0028 & 8.9052 \\ \hline B & 1.4189 & 8.0411 \\ \hline B & 4.2176 & 2.0826 \\ \hline B & 9.1574 & 1.0536 \\ \hline B & 7.9221 & 9.0649 \\ \hline B & 9.5949 & 10.0826 \\ \hline \end{tabular}$

Ci-dessous le nuage de points basé sur ces données,

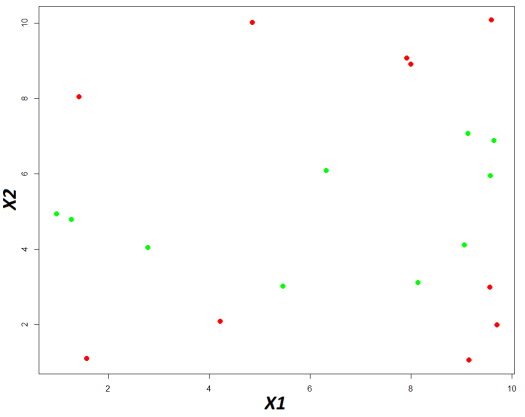
En vert la classe « A » et en rouge la classe « B »

On cherche donc à modéliser $Y$ en fonction des valeurs de $(X ^1, X ^2)$ . Comme il s’agit d’un exemple, on s’affranchira de la construction par apprentissage statistique.

On applique sur $X ^1$ une B-spline à $5$ degrés de liberté ( $ddl$ ) et $1$ degré pour le polynôme local ( $d$ ). Pour commencer, on détermine arbitrairement le vecteur de $5$ nœuds, soit les $ddl$ paramétrés, selon un découpage homogène :

$q = (min, Q_{20 \%}, Q_{40 \%}, Q_{60 \%}, Q_{80 \%}, max) = (0.9754, 2.54322, 5.98168, 8.51148, 9.57238, 9.5751)$

Pour chaque nœud, on calcule les valeurs de : $X_1 ^1 = 8.1472$ , ce qui implique que l’on va devoir développer cinq composantes.

Pour la première composante :

$B_{1,d = 1} (X_1 ^1) = \frac{X_1 ^1 - q_1}{q_{1+1} - q_1} \cdot B_{1,1-1} (X_1 ^1) + \frac{q_{1+1+1} - X_1 ^1}{q_{1+1+1} - q_{1+1}} \cdot B_{1+1,1-1} (X ^1)$

$= \frac{X_1 ^1 - q_1}{q_2 - q_1} \cdot B_{1,0} (X_1 ^1) + \frac{q_3 - X_1 ^1}{q_3 - q_2} \cdot B_{2,0} (X_1 ^1)$

, or par définition $\forall t \in \lbrace 1, \cdots, 5 \rbrace, B_{t,0} (X ^1) = 1$ si $q_t < X ^1 < q_{t+1}$ , $0$ sinon. On a $q_1 = min(X ^1) = 0.9754$ , $q_2 = Q_{20 \%} = 2.54322$ .et $q_3 = Q_{40 \%} = 5.98168$ .

$B_{1,d = 1} (X_1 ^1) = \frac{X_1 ^1 - q_1}{q_2 - q_1} \times 0 + \frac{q_3 - X_1 ^1}{q_3 - q_2} \times 0 = 0$

, puisque $X_1 ^1 = 8.1472 \notin ]0.9754, 2.54322[$ et $\notin ]2.54322, 5.98168[$ .

Ensuite, on calcul la seconde composante avec $q_2 = Q_{20 \%} = 2.54322$ , $q_3 = Q_{40 \%} = 5.98168$ et $q_4 = Q_{60 \%} = 8.51148$ :

$B_{2,d = 1} (X_1 ^1) = \frac{X_1 ^1 - q_2}{q_3 - q_2} \times 0 + \frac{q_4 - X_1 ^1}{q_4 - q_3} \times 1 = \frac{8.51148 - 8.1472}{8.51148 - 5.98168} = 0.1439956$

, puisque $X_1 ^1 = 8.1472 \notin ]2.54322, 5.98168[$ et $\in ]5.98168, 8.51148[$ .

Ensuite, on calcul la troisième composante avec $q_3 = Q_{40 \%} = 5.98168$ , $q_4 = Q_{60 \%} = 8.51148$ et $q_5 = Q_{80 \%} = 9.57238$ :

$B_{3,d = 1} (X_1 ^1) = \frac{X_1 ^1 - q_3}{q_4 - q_3} \times 1 + \frac{q_5 - X_1 ^1}{q_5 - q_4} \times 0 = \frac{8.1472 - 5.98168}{8.51148- 5.98168} = 0.856004$

, puisque $X_1 ^1 = 8.1472 \in ]5.98168, 8.51148[$ et $\notin ]8.51148, 9.57238[$ .

Puis, on calcul la quatrième composante avec $q_4 = Q_{60 \%} = 8.51148$ , $q_5 = Q_{80 \%} = 9.57238$ et $q_6 = max = 9.5751$ :

$B_{4,d = 1} (X_1 ^1) = \frac{X_1 ^1 - q_4}{q_5 - q_4} \times 0 + \frac{q_6 - X_1 ^1}{q_6 - q_5} \times 0 = 0$

, puisque $X_1 ^1 = 8.1472 \notin ]8.51148, 9.57238[$ et $\notin ]9.57238, 9.5751[$ .

Et enfin, la cinquième composante :

$B_{5, d = 1} = 1 - (B_{1, d = 1} + B_{2, d = 1} + B_{3, d = 1} + B_{4, d = 1})$

$= 0 + 0.1439956 + 0.8560044 + 0$

$= 0$

D’où,

$(B_{d = 1})_1 (X ^1) = (0, 0.1439956, 0.8560044, 0, 0)$

On généralise la méthode de calcul à tous les éléments de $X ^1$ et on obtient la matrice suivante :

$\mathbf{B}_{d = 1} = \begin{pmatrix} 0 & 0.1439956 & 0.8560044 & 0 & 0 \\ 0 & 0 & 0.4849467 & 0.5150533 & 0 \\ 0.1878404 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0.4134037 & 0.5865963 & 0 \\ 0 & 0.8648431 & 0.1351569 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0.9296836 & 0.0703164 & 0 & 0 & 0 \\ 0.1491598 & 0.8508402 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0.9796285 & 0.0203715 \\ 0 & 0 & 0 & 0.4269023 & 0.5730977 \\ 0.3831435 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0.0006410 & 0.9993590 & 0 \\ 0.3280189 & 0.6719811 & 0 & 0 & 0 \\ 0 & 0.2010752 & 0.7989248 & 0 & 0 \\ 0.2828769 & 0 & 0 & 0 & 0 \\ 0.5130436 & 0.4869564 & 0 & 0 & 0 \\ 0 & 0 & 0.3911585 & 0.6088415 & 0 \\ 0 & 0.2329749 & 0.7670251 & 0 & 0 \\ 0 & 0 & 0 & 0.8313361 & 0.1686639 \\ \end{pmatrix}$

On va maintenant appliquer la régression logistique de $Y$ sur $(\mathbf{B}_{d = 1}, X ^2)$ afin de déterminer les coefficients associés aux composantes B-spline de $X ^1$ et à la forme non-transformée de $X ^2$ .

On pourra alors consulter cette article qui détaille l’algorithme de calcul : https://lemakistatheux.wordpress.com/category/outils-danalyse-supervisee/la-regression-logistique/

On obtient les résultats qui suivent :

$\begin{tabular}{|l|c|c|} \hline Variable & Transformation & Coefficient \\ \hline Intercept & & -1.0591 \\ \hline X1 & B-spline composante 1 & 1.5927 \\ \hline & B-spline composante 2 & -0.1434 \\ \hline & B-spline composante 3 & 0.7526 \\ \hline & B-spline composante 4 & 0.3680 \\ \hline & B-spline composante 5 & 1.6194 \\ \hline X2 & & 0.0925 \\ \hline \end{tabular}$

Les performances obtenues peuvent être décrites au travers de la matrice de confusion suivante :

$\begin{tabular}{|l|c|c|} \hline & Prediction = A & Pr\'ediction = B \\ \hline Observ\'e = A & 7 & 3 \\ \hline Observ\'e = B & 4 & 6 \\ \hline \end{tabular}$

, soit un taux de bonne classification globale de $65 \%$ . Enfin, et plus concrètement, on peut afficher le découpage du plan comparé aux classes réelles.

Les bandes rouges correspondent à la région de la classe « A » construite par le modèle, en bleu celle de la classe « B ». En rouge les données réelles de la classe « A » et en vert celles de la classe « B »

$\bullet$ Application sous R :

Soit l’exemple suivant :

E = data.frame(Y = c(rep(0,10),rep(1,10)),
X1 = c(8.1472, 9.0579, 1.2699, 9.1338, 6.3236, 0.9754, 2.7850, 5.4688, 9.5751, 9.6489, 1.5761, 9.7059, 9.5717, 4.8538, 8.0028, 1.4189, 4.2176, 9.1574, 7.9221, 9.5949),
X2 = c(3.1101, 4.1008, 4.7876, 7.0677, 6.0858, 4.9309, 4.0449, 3.0101, 5.9496, 6.8729, 1.0898, 1.9868, 2.9853, 10.0080, 8.9052, 8.0411, 2.0826, 1.0536, 9.0649, 10.0826))

Package et fonction R: https://stat.ethz.ch/R-manual/R-devel/library/mgcv/html/gam.html

La fonction gam du package mgcv permet de réaliser des modèles additifs généralisés. Après chargement du package, on lance la construction du modèle de la manière suivante :

model = gam(Y ~ bs(X1, df = 5, degree = 1) + X2, data = E, family = binomial(link = « logit »))

summary(model)

Parmi les éléments à insérer les plus importants il faut relever :

– La formule définissant variable réponse (à gauche) et variables explicatives (à droite) : $Y$ ~ $bs(X1, df = 5, degree = 1) + X2$ , on remarquera que cette dernière contient directement l’application de la fonction de lissage (ici une B-spline) sur $X ^1$ tandis que pour $X ^2$ on prendra sa forme d’origine. Enfin, à noter que $Y$ doit être codée $\lbrace 0, 1 \rbrace$ ;

– La base de données sur laquelle on souhaite travailler : $data = E$ ;

– La fonction lien : $family = binomial(link = "logit")$ ;

– La production de tous les détails du modèle construit : $summary(model)$ .

On obtient alors les résultats suivants :

On vérifie :

– La fonction lien : « Family : binomial », « Link function: logit » ;

– Le modèle paramétré : « Y ~ bs(X1, df = 5, degree = 1) + X2 » ;

– Les coefficients associés aux dérivations de $X ^1$ et à $X ^2$ dans la première colonne , qui sont les mêmes que ceux obtenus lors des calculs manuels (cf section « Exemple ») ;

– Le niveau de significativité de chaque coefficient dans la dernière colonne : « Pr(>|Z|) » ;

– Et les performances du modèle sur les deux dernières lignes.

$\bullet$ Application sous SAS :

Soit l’exemple suivant :

data E;
input x1 x2 Y $1.;
cards;
8.1472 3.1101 A
9.0579 4.1008 A
1.2699 4.7876 A
9.1338 7.0677 A
6.3236 6.0858 A
0.9754 4.9309 A
2.7850 4.0449 A
5.4688 3.0101 A
9.5751 5.9495 A
9.6489 6.8729 A
1.5761 1.0898 B
9.7059 1.9868 B
9.5717 2.9853 B
4.8538 10.0080 B
8.0028 8.9052 B
1.4189 8.0411 B
4.2176 2.0826 B
9.1574 1.0536 B
7.9221 9.0649 B
9.5949 10.0826 B
;
run;

Procédure SAS: https://support.sas.com/documentation/cdl/en/statug/63033/HTML/default/viewer.htm#statug_gam_sect004.htm

La procédure GAM permet de réaliser des modèles additifs généralisés, toutefois elle n’offre pas un choix aussi varié que sous R. On lance la construction du modèle de la manière suivante :

proc gam data = E;
model Y (event = « B ») = spline(X1,df = 5) param(X2) / link = binomial;
ods exclude ConvergenceStatus InputSummary IterSummary ResponseProfile;
run;

Parmi les éléments à insérer les plus importants il faut relever :

– La base de données sur laquelle on souhaite travailler : $data = E$ ;

– La formule définissant variable réponse (à gauche) et variables explicatives (à droite) : $model$ $Y (event = "B") = spline(X1, df = 5)$ $param(X2)$ , on remarquera que cette dernière contient directement l’application de la fonction de lissage (ici une spline) sur $X ^1$ tandis que pour $X ^2$ on prendra sa forme d’origine ;

– La fonction lien : $/ link = binomial$ ;

– L’ODS output est utilisé afin de ne filtrer que les résultats d’intérêt.

On obtient alors les résultats suivants :

On vérifie :

– Dans le premier tableau, la liste des coefficients associés à chaque variable brute du modèle $X ^1$ et $X ^2$ , le manque de possibilité comparé à R fait que l’on aura appliqué ici un paramétrage différent non comparable à celui des calculs manuels ;

– Dans le deuxième tableau, le coefficient associé à la transformation de $X ^1$ , le manque de possibilité comparé à R fait que l’on aura appliqué ici un paramétrage différent non comparable à celui des calculs manuels ;

– Dans le troisième tableau, les indicateurs de performance de la version transformée de $X ^1$ .

$\bullet$ Bibliographie :

– The Elements of Statistical Learning de Trevor Hastie, Robert Tibshirani et Jerome Friedman ;

– Data Mining et statistique décisionnelle. L’Intelligence des données de Stéphane Tufféry.

lemakistatheux

Youhou Mayotte c'est la fête…

Archives de Tag: GAM

Le modèle additif généralisé