MARS – lemakistatheux

Yoav Freund (à gauche) et Robert Shapire (à droite)

$\bullet$ Historique :

$\begin{tabular}{|l|c|c|} \hline Bloc & 07/12/2016-V1 & 13/03/2024-V2 \\ \hline Historique & & Cr\'eation \\ \hline Sommaire & & Cr\'eation \\ \hline Pr\'esentation & Cr\'eation & \\ \hline Les algorithmes de boosting & Cr\'eation & Devient Le Boosting \\ \hline Annexe th\'eorique & Cr\'eation & \\ \hline Exemple & & Cr\'eation \\ \hline Appli... Informatique & Cr\'eation & Devient Appli... sous R \\ \hline Appli... sous SAS & & Cr\'eation \\ \hline Bibliographie & Cr\'eation & \\ \hline \end{tabular}$

$\bullet$ Sommaire :

Présentation
Le Boosting
- Le concept général
- L’algorithme AdaBoost
- L’algorithme MARS
Annexe théorique
Exemple
Application sous R
Application sous SAS
Bibliographie

$\bullet$ Présentation :

Le Boosting est une famille d’outils d’analyse discriminante très puissants. L’idée est d’améliorer la règle de discrimination d’un classifieur sur plusieurs sous-parties de l’hyperplan formé par $(Y, X ^1, \cdots, X ^P)$ et d’établir la classification finale au travers d’un vote global pondéré. Chaque partie du plan se voit alors attribuer une pondération en fonction de sa performance de discrimination mise à jour itération par itération afin d’adapter la frontière décisionnelle en fonction des zones les plus difficiles à classer.

Le classifieur utilisé est la plupart du temps la régression linéaire, logistique ou les arbres de décision. Ils portent le nom de « classifieurs fiables » à la fois car ils sont simples d’utilisation mais également car l’objectif du Boosting est d’améliorer la règle de discrimination lorsqu’elle est peu performante.

Le Boosting appartient à la catégorie des méthodes d’apprentissage statistique nécessitant un jeu de d’apprentissage pour la conception de la règle d’apprentissage et un jeu de test pour sa validation afin de limiter les risques de sur-apprentissage. Comme la plupart d’entre elles, il a le principal défaut de concevoir une règle décisionnelle peu lisible d’où son surnom de boîte noire.

Parmi les méthodes de Boosting, la plus célèbre reste l’algorithme AdaBoost conçu par Yoav Freun et Robert Shapire en 1997 et définit pour la discrimination d’une variable réponse $Y$ binaire à partir d’un ensemble de variables continues explicatives $\mathbf{X} = (X ^1, \cdots, X ^P)$ . D’autres algorithmes de Boosting sont également particulièrement répandus, on peut ainsi citer : l’algorithme Gentle Adaboost, Real Adaboost, MART et RankBoost.

$\bullet$ Les algorithmes de Boosting :

Hypothèse préliminaire: $Y$ binaire ou continue, $\mathbf{X}$ continue.

Le concept général

Avant d’aborder les algorithmes Adaboost et MART, on présentera l’algorithme de Boosting de base.

– Étape initiale : Définir un classifieur faible $f(.)$ , une fonction de coût $Pr().$ , un nombre $T$ d’itérations d’entrainement pour l’optimisation des pondérations. On définit enfin $w ^0$ les poids d’origine que l’on fixe à la même valeur quelque soit l’observation.

– Étapes itératives : Pour $t \in \lbrace 1, \cdots, T \rbrace$ ,

Étape 1 : On apprend le modèle, selon apprentissage statistique via tirage pondéré par les $w ^{t-1}$ .
Étape 2 : On applique le modèle construit, sur le sous-échantillon des observations qui n’ont pas été tirées à la première étape, aussi les $w ^{t-1}$ ne sont pas réutilisés ici, et on récupère les prédictions obtenues : $\hat{Y_t}$ . Point important, si l’on ne souhaite pas utiliser d’apprentissage statistique alors ces deux premières étapes sont réalisées en même temps, on lance le classifieur faible directement en prenant en compte les $w ^{t-1}$ .
Étape 3 : On mesure le taux d’erreurs de classification de la règle décisionnelle conçue précédemment par la fonction de coût : $\epsilon_t = Pr(I_{[\hat{Y_t} \neq Y]})$ .
Étape 4 : On met à jour les pondérations $w ^{t-1}$ , chaque observation mal classée se voit alors attribuer un poids plus important, ce qui donne $w ^t$ .

– Étape finale : On détermine la règle décisionnelle finale par vote sur $\hat{Y}_t, \forall t \in [1,T]$

L’algorithme AdaBoost

Pensé pour le cas où $Y$ est binaire, AdaBoost utilisera l’arbre de décision comme classifieur faible. On n’évoquera pas l’utilisation de l’apprentissage statistique ici qui est le même que pour le concept général décrit ci-avant. L’Algorithme se décline de la manière suivante :

– Étape initiale : Initialisation des pondérations associées aux observations,

$w_i ^0 = \frac{1}{n}, \forall i \in [1,n]$

– Étapes itératives : $\forall t \in [1,T]$

Étape 1-2 : Détermination, selon apprentissage statistique, des prédictions $\hat{Y}_t$ en prenant en compte les poids $w ^{t-1}$ ;
Étape 3 : Calcul du taux d’erreurs : $\sum_{i = 1} ^{n} w_i ^t \cdot \lbrace \hat{Y}_i \neq Y_i \rbrace$ ;
Étape 4 : Si $\epsilon_t >0.5$ alors le classifieur fait mieux qu’une règle aléatoire et on conserve le modèle, sinon on ajuste,
- Le coefficient de pondération selon ses deux variantes :

La méthode de Breiman, $\alpha_t = \frac{1}{2} \cdot ln(\frac{1 - \epsilon_t}{\epsilon_t})$

La méthode de Zhu pour le cas binaire, $\alpha_t = ln(\frac{1 - \epsilon_t}{\epsilon_t})$

- Les pondérations :

$w_i ^t = w_i ^{t - 1} e ^{\alpha_t \cdot I_{(\hat{Y}_i \neq Y_i)}}, \forall i \in [1,n]$

– Étape finale : On obtient le modèle final,

$H(x) = sign[\sum_{t = 1} ^T \alpha_t f_t (x)]$

L’Algorithme MART

L’Algorithme Multiple Additive Regression Trees se base sur l’utilisation d’arbres de régression. Par conséquent, il est adapté au cas où $Y$ est continue. On n’évoquera pas l’utilisation de l’apprentissage statistique ici qui est le même que pour le concept général décrit ci-avant. Les différentes étapes d’estimation sont les suivantes :

– Étape initiale : Initialiser $f_0 (x) = arg min_{\delta} \sum_{i = 1} ^N L(y_i, \delta)$ , avec $L$ fonction de perte à minimiser, et choix du nombre d’itérations $T$ .

– Étapes itératives : Pour $t \in [1, T]$ ,

Étape 1 : Pour $i \in [1, n]$ calculer,

$r_{i,t} = - [\frac{\partial L(y_i, f(x_i))}{\partial f(x_i)}]_{f = f_{t - 1}}$

Étape 2 : Estimer le modèle par arbre de régression sur $r_{i,t}$ et donnant les régions décisionnelles $R_{j,t}, \forall j \in \lbrace 1, \cdots, J_t \rbrace$
Étape 3 : Pour $j \in \lbrace 1, \cdots, J_t \rbrace$ , calculer,

$\delta_{j,t} = arg min_{\delta} \sum_{x_i \in R_{j,t}} L(y_i, f_{t - 1} (x_i) + \delta)$

Étape 4 : Mettre à jour $f_t (x) = f_{t - 1} (x) + \sum_{j = 1} ^{J_t} \delta_{j,t} I (x \in R_{j,t})$

– Étape 2 : On a enfin la règle décisionnelle finale de forme $\hat{f} (x) = f_T (x)$

$\bullet$ Annexe théorique :

Cette partie de l’article présente une esquisse de la justification de l’usage de la fonction de perte exponentielle.

L’algorithme AdaBoost se base sur l’idée nouvelle d’une fonction de perte exponentielle dont le principal avantage est computationnel. En partant du principe que $Y \in \lbrace -1, 1 \rbrace$ , on montre facilement que,

$f ^* (x) = arg min_{f(x)} E_{Y|x} (e ^{-Y f(x)}) = \frac{1}{2} log \frac{P(Y = 1 | x)}{P(Y = -1 | x)}$

Et équivalent à,

$P(Y = 1 | x) = \frac{1}{1 + e ^{-2 f^* (x)}}$

De cette manière, l’expansion additive produite par l’algorithme AdaBoost revient à estimer une partie du log-odds de $P(Y = 1 | x)$ . Ce qui justifie l’usage de son signe comme règle de classification décrite par la formule,

$G(x) = sign (\sum_{m = 1} ^M \alpha_m G_m (x))$

Un autre critère de minimisation de perte est la log-vraisemblance de la loi binomiale négative (appelée également déviance ou entropie croisée), interprétant $f$ comme une transformation logit. On a,

$p(x) = P(Y = 1 | x) = \frac{e ^{f(x)}}{e ^{-f(x)} + e ^{f(x)}} = \frac{1}{1 + e ^{-2 f(x)}}$

, avec $Y ' = \frac{Y + 1}{2} \in \lbrace 0, 1 \rbrace$ . La fonction de perte est alors,

$l(Y,p(x)) = Y ' log (p(x)) + (1 - Y ') log(1 - p(x))$

Et de déviance,

$-l (Y, f(x)) = log (1 + e ^{-2Y f(x)})$

De la formule précédente, on voit que,

$E_{Y|x} [-l(Y,f(x))] = E_{Y|x} [e ^{-Y f(x)}]$

$\bullet$ Exemple :

Soit l’échantillon $(Y, X ^1, X ^2)$ suivant,

$\begin{tabular}{|c|c|c|} \hline Y & X1 & X2 \\ \hline A & 8.1472 & 3.1101 \\ \hline A & 9.0579 & 4.1008 \\ \hline A & 1.2699 & 4.7876 \\ \hline A & 9.1338 & 7.0677 \\ \hline A & 6.3236 & 6.0858 \\ \hline A & 0.9754 & 4.9309 \\ \hline A & 2.7850 & 4.0449 \\ \hline A & 5.4688 & 3.0101 \\ \hline A & 9.5751 & 5.9496 \\ \hline A & 9.6489 & 6.8729 \\ \hline B & 1.5761 & 1.0898 \\ \hline B & 9.7059 & 1.9868 \\ \hline B & 9.5717 & 2.9853 \\ \hline B & 4.8538 & 10.0080 \\ \hline B & 8.0028 & 8.9052 \\ \hline B & 1.4189 & 8.0411 \\ \hline B & 4.2176 & 2.0826 \\ \hline B & 9.1574 & 1.0536 \\ \hline B & 7.9221 & 9.0649 \\ \hline B & 9.5949 & 10.0826 \\ \hline \end{tabular}$

Ci-dessous le nuage de point basé sur ces données,

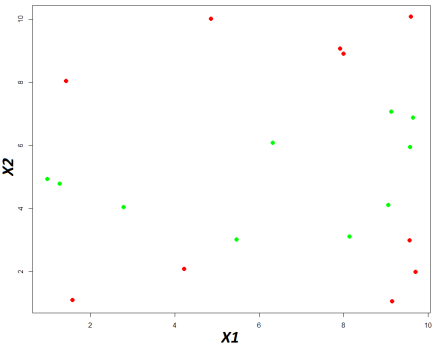
En vert la classe « A » et en rouge la classe « B »

On cherche donc à déterminer une fonction permettant de prédire les deux classes de $Y$ en fonction des valeurs de $(X ^1, X ^2)$ . Comme il s’agit d’un exemple, on s’affranchira de la construction par apprentissage statistique.

On démarre en fixant les paramètres :

Le classifieur faible sera l’arbre décisionnel, conformément au concept de l’AdaBoost, pour lequel on acceptera uniquement une profondeur d’un seul niveau ;
L’échantillon complet servira de base d’apprentissage à chaque itération, comprendre que la règle produite le sera sur les $20$ observations ;
On utilisera la méthode de Breiman pour le calcul du taux d’erreur ;
On initialise tous les poids à $w ^0 = \frac{1}{20} = 0.05$ pour chaque observation ;
On choisit $10$ itérations pour la convergence du modèle.

Maintenant on peut lancer la procédure itérative $t = 1$ . On obtient le modèle suivant :

, et de performance de classification :

$\begin{tabular}{|l|c|c|} \hline & Prediction = A & Pr\'ediction = B \\ \hline Observ\'e = A & 8 & 2 \\ \hline Observ\'e = B & 5 & 5 \\ \hline \end{tabular}$

Soit un taux de mauvaise classification pondérée de :

$\epsilon_1 = \sum_{i = 1} ^{20} w_i ^0 \times \lbrace Y_i \neq \hat{Y}_i \rbrace = 0.05 + 0 + 0 + 0 + 0 + 0 + 0 + 0.05 + 0 + \cdots = 35 \%$

, $w_i ^0 \times 0 = 0$ lorsque prédiction pour l’observation $i$ ne correspond pas à la classe réelle, et $w_i ^0 \times 1 = w_i ^0$ lorsque c’est le cas.

Comme on utilise la méthode de Breiman, alors l’erreur corrigée vaut :

$\alpha_1 = \frac{1}{2} \times log(\frac{1 - \epsilon_1}{\epsilon_1}) = \frac{1}{2} \times log(1.857143) = \frac{1}{2} \times 0.6190392 = 0.3095196$

, que l’on propage ensuite pour rectifier le vecteur des pondérations $w ^0$ ,

$w ^{build} = w ^0 \times e ^{\alpha_1 \times \lbrace Y_i \neq \hat{Y}_i \rbrace} = \begin{pmatrix} 0.05 \times e ^{0.3095196} \\ 0.05 \times e ^0 \\ 0.05 \times e ^0 \\ 0.05 \times e ^0 \\ 0.05 \times e ^0 \\ 0.05 \times e ^0 \\ 0.05 \times e ^0 \\ 0.05 \times e ^{0.3095196} \\ 0.05 \times e ^0 \\ 0.05 \times e ^0 \\ 0.05 \times e ^0 \\ 0.05 \times e ^0 \\ 0.05 \times e ^0 \\ 0.05 \times e ^{0.3095196} \\ 0.05 \times e ^{0.3095196} \\ 0.05 \times e ^{0.3095196} \\ 0.05 \times e ^0 \\ 0.05 \times e ^0 \\ 0.05 \times e ^{0.3095196} \\ 0.05 \times e ^{0.3095196} \end{pmatrix} = \begin{pmatrix} 0.06813851 \\ 0.05 \\ 0.05 \\ 0.05 \\ 0.05 \\ 0.05 \\ 0.05 \\ 0.06813851 \\ 0.05 \\ 0.05 \\ 0.05 \\ 0.05 \\ 0.05 \\ 0.06813851 \\ 0.06813851 \\ 0.05 \\ 0.05 \\ 0.6813851 \\ 0.06813851 \end{pmatrix}$

Enfin, on applique la dernière correction en divisant $w ^{build}$ par :

$\frac{1}{\sum_{i = 1} ^{20} w_i ^{build}} = \frac{1}{1.12697}$

, d’où,

$w ^1 = \frac{1}{1.12697} \times w ^{build} = \begin{pmatrix} 0.06046171 \\ 0.04436677 \\ 0.04436677 \\ 0.04436677 \\ 0.04436677 \\ 0.04436677 \\ 0.04436677 \\ 0.06046171 \\ 0.04436677 \\ 0.04436677 \\ 0.04436677 \\ 0.04436677 \\ 0.04436677 \\ 0.06046171 \\ 0.06046171 \\ 0.06046171 \\ 0.04436677 \\ 0.04436677 \\ 0.06046171 \\ 0.06046171 \end{pmatrix}$

On vient de boucler la première itération. On lance maintenant la seconde $t = 2$ en reprenant alors les mêmes étapes. On obtient le même arbre de décision mais pour le cutoff : $X ^2 < 6.47935$ , ainsi que les mêmes performances. Soit un taux de mauvaise classification pondérée de :

$\epsilon_2 = \sum_{i = 1} ^{20} w_i ^1 \times \lbrace Y_i \neq \hat{Y}_i \rbrace$

$= 0 + 0 + 0 + 0.0443667 + 0 + 0 + 0 + 0 + 0 + \cdots$

$= 31.05674 \%$

On calcule ensuite l’erreur corrigée :

$\alpha_2 = \frac{1}{2} \times log(\frac{1 - \epsilon_2}{\epsilon_2}) = 0.398734$

, que l’on propage ensuite pour rectifier le vecteur des pondérations $w ^1$ ,

$w ^{build} = w ^1 \times e ^{erreur \times \lbrace Y_i \neq \hat{Y}_i \rbrace} = \begin{pmatrix} 0.06046171 \times e ^0 \\ 0.0443667 \times e ^0 \\ 0.0443667 \times e ^0 \\ 0.0443667 \times e ^{0.398734} \\ 0.0443667 \times e ^0 \\ 0.0443667 \times e ^0 \\ 0.0443667 \times e ^0 \\ 0.06046171 \times e ^{0.3095196} \\ 0.0443667 \times e ^0 \\ 0.0443667 \times e ^0 \\ 0.0443667 \times e ^0 \\ 0.0443667 \times e ^0 \\ 0.0443667 \times e ^0 \\ 0.06046171 \times e ^{0.3095196} \\ 0.0443667 \times e ^{0.3095196} \\ 0.06046171 \times e ^{0.3095196} \\ 0.06046171 \times e ^0 \\ 0.06046171 \times e ^0 \\ 0.06046171 \times e ^{0.3095196} \\ 0.06046171 \times e ^{0.3095196} \end{pmatrix} = \begin{pmatrix} 0.06046171 \\ 0.04436677 \\ 0.0443667 \\ 0.06610370 \\ 0.0443667 \\ 0.0443667 \\ 0.0443667 \\ 0.06046171 \\ 0.0443667 \\ 0.06610370 \\ 0.06610370 \\ 0.06610370 \\ 0.06046171 \\ 0.06046171 \\ 0.06046171 \\ 0.05 \\ 0.05 \\ 0.06046171 \\ 0.06046171 \end{pmatrix}$

Enfin, on applique la dernière correction en divisant $w ^1$ par :

$\frac{1}{\sum_{i = 1} ^{20} w_i ^{build}} = \frac{1}{1.053847}$

, d’où :

$w ^1 = \frac{1}{1.053847} \times w ^{build} = \begin{pmatrix} 0.05247691 \\ 0.03850752 \\ 0.03850752 \\ 0.08548335 \\ 0.03850752 \\ 0.03850752 \\ 0.03850752 \\ 0.05247691 \\ 0.03850752 \\ 0.08548335 \\ 0.08548335 \\ 0.08548335 \\ 0.08548335 \\ 0.05247691 \\ 0.05247691 \\ 0.05247691 \\ 0.08548335 \\ 0.08548335 \\ 0.05247691 \\ 0.05247691 \end{pmatrix}$

On poursuit ainsi jusqu’à parcourir les $8$ autres itérations paramétrées, et en mettant à jour les pondérations. On obtient ainsi la matrice de classification à chaque itération suivante :

$\hat{Y}_T = \begin{pmatrix} t1 & t2 & t3 & t4 & t5 & t6 & t7 & t8 & t9 & t10 \\ 0 & 1 & 0 & 1 & 0 & 1 & 0 & 0 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 & 0 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 & 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 & 1 & 0 & 0 & 1 & 1 & 0 \\ 1 & 1 & 1 & 1 & 1 & 1 & 0 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 & 0 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 & 0 & 1 & 0 & 1 \\ 0 & 1 & 0 & 1 & 0 & 1 & 0 & 0 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 & 0 & 1 & 1 & 1 \\ 1 & 0 & 1 & 0 & 1 & 0 & 0 & 1 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 1 & 0 & 1 & 0 & 0 & 1 & 1 \\ 0 & 1 & 0 & 1 & 0 & 1 & 0 & 0 & 1 & 1 \\ 1 & 0 & 1 & 0 & 1 & 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 1 & 0 & 1 & 0 & 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 0 & 1 & 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 1 & 0 & 1 & 0 & 0 & 1 & 1 \\ 1 & 0 & 1 & 0 & 1 & 0 & 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 0 & 1 & 0 & 0 & 1 & 1 & 0 \end{pmatrix}$

, et le vecteur des erreurs corrigées :

$\alpha = (0.3095196, 0.398734, 0.2718262, 0.2870794, 0.2316742, 0.224702, 0.2129758, 0.2168389, 0.1676402 0.2136311)$

On procède au produit suivant afin de déterminer les scoring pour chaque observation :

$\hat{Y} = (Classif \cdot \alpha, (1 - Classif) \cdot \alpha) = \begin{pmatrix} Y = A & Y = B \\ 1.291787 & 1.2428347 \\ 2.321646 & 0.2129758 \\ 2.154005 & 0.3806160 \\ 1.197499 & 1.3371223 \\ 2.321646 & 0.2129758 \\ 2.154005 & 0.3806160 \\ 2.154005 & 0.3806160 \\ 1.291787 & 1.2428347 \\ 2.321646 & 0.2129758 \\ 1.197499 & 1.3371223 \\ 1.124146 & 1.4104749 \\ 1.291787 & 1.2428347 \\ 1.291787 & 1.2428347 \\ 1.029859 & 1.5047624 \\ 1.197499 & 1.3371223 \\ 1.029859 & 1.5047624 \\ 1.124146 & 1.4104749 \\ 1.291787 & 1.2428347 \\ 1.197499 & 1.3371223 \\ 1.197499 & 1.3371223 \end{pmatrix}$

En attribuant la classe finale en fonction de la valeur la plus importante on obtient les performances décrites au travers de la matrice de confusion suivante :

$\begin{tabular}{|l|c|c|} \hline & Prediction = A & Pr\'ediction = B \\ \hline Observ\'e = A & 8 & 3 \\ \hline Observ\'e = B & 2 & 7 \\ \hline \end{tabular}$

, soit un taux de bonne classification globale de $75 \%$ . Enfin, et plus concrètement, on peut afficher le découpage du plan comparé aux classes réelles.

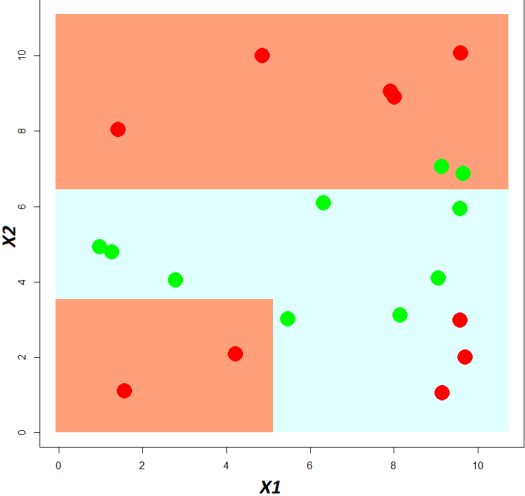
Les bandes rouges correspondent à la région de la classe « A » construite par le modèle, en bleu celle de la classe « B ». En rouge les données réelles de la classe « A » et en vert celles de la classe « B »

$\bullet$ Application sous R :

Soit l’exemple suivant :

E = data.frame(Y = c(rep(0,10),rep(1,10)),
X1 = c(8.1472, 9.0579, 1.2699, 9.1338, 6.3236, 0.9754, 2.7850, 5.4688, 9.5751, 9.6489, 1.5761, 9.7059, 9.5717, 4.8538, 8.0028, 1.4189, 4.2176, 9.1574, 7.9221, 9.5949),
X2 = c(3.1101, 4.1008, 4.7876, 7.0677, 6.0858, 4.9309, 4.0449, 3.0101, 5.9496, 6.8729, 1.0898, 1.9868, 2.9853, 10.0080, 8.9052, 8.0411, 2.0826, 1.0536, 9.0649, 10.0826))

Package et fonction R :

La fonction boosting du package adabag permet d’appliquer l’algorithme AdaBoost. Après chargement du package, on lance sa conception de la manière suivante :

boosting(Y ~ X1+X2, data = E, boos = FALSE, mfinal = 10, coeflearn = « Breiman », control = rpart.control(minsplit = 7,minbucket=7))

Parmi les éléments à insérer les plus importants il faut relever :

– La formule définissant variable réponse (à gauche) et variables explicatives (à droite) : $Y$ ~ $X1 + X2$ ;

– La base de données sur laquelle on souhaite travailler : $data = E$ ;

– La non utilisation d’un échantillonnage à chaque itération : $boos = FALSE$ ;

– Le nombre d’itérations total : $mfinal = 10$ ;

– La correction de Breiman lors du calcul de l’erreur à chaque itération : $coeflearn = "Breiman"$ ;

– Le paramétrage du classifieur faible qui sous R est obligatoirement l’arbre de décision : $control = rpart.control(minsplit = 7, minbucket = 7)$ .

On obtient alors les résultats suivants :

On vérifie,

– Dans les sorties de type : $\$trees[[.]]$ , les différents arbres de décisions conçus à chaque itération (on a volontairement tronqué la sortie), et qui sont les mêmes que ceux obtenus lors des calculs manuls (cf partie « Exemple ») ;

– La somme des erreurs composants le vecteur $erreur$ à chaque itération : $\$weight$ , qui sont les mêmes que celles obtenues lors des calculs manuls (cf partie « Exemple ») ;

– La valeur finale des votes par observation : $\$votes$ (la sortie $\$prob$ étant le résultat de chaque valeur divisé par la somme en ligne), qui sont les mêmes que ceux obtenus lors des calculs manuls (cf partie « Exemple ») ;

– Les classifications finales attribuées : $\$class$ , qui sont les mêmes que celles obtenues lors des calculs manuls (cf partie « Exemple ») ;

– Le poids d’influence des différentes variables du modèles : $\$importance$ ;

– Les autres sorties indiquent le paramétrage de la fonction.

$\bullet$ Application sous SAS :

Soit l’exemple suivant :

data BDD;
input x1 x2 Y;
cards;
8.1472 3.1101 A
9.0579 4.1008 A
1.2699 4.7876 A
9.1338 7.0677 A
6.3236 6.0858 A
0.9754 4.9309 A
2.7850 4.0449 A
5.4688 3.0101 A
9.5751 5.9495 A
9.6489 6.8729 A
1.5761 1.0898 B
9.7059 1.9868 B
9.5717 2.9853 B
4.8538 10.0080 B
8.0028 8.9052 B
1.4189 8.0411 B
4.2176 2.0826 B
9.1574 1.0536 B
7.9221 9.0649 B
9.5949 10.0826 B
;
run;

Il n’existe pas de procédure sous SAS permettant de lancer le Boosting. Par conséquent, on proposera la macro suivante :

%macro Boosting(DATA =, Y =, Classifieur =, FctCout = , Iteration = );

/* La macro ici présente permet d’appliquer l’algorithme AdaBoost en prenant pour classifieur faible la régression logistique.

Les paramètres utilisés sont :

– DATA, la base de données

– Y, la variable réponse binaire, par défaut toutes les autres variables seront utilisées pour la modélisation

– Classifieur, le type de classifieur faible, pour cette première version seule l’option LOG pour la régression logistique est disponible

– FctCout, la fonction erreur, pour cette première version seule celle de Breiman est disponible

– Iteration, le nombre d’itérations à utiliser pour le calcul des poids */

/* Options pour épurer la log */

options nonotes spool;

/* On rajoute 1 au paramètre ITERATION pour automatiser la classification finale en fait */

%let Itefin = %eval(&Iteration. + 1);

/* Récupération de la taille de l’échantillon */

proc sql noprint;

select count(*) into: n from &DATA.;

quit;

/* Récupération de la liste des variables autre que la réponse pour ériger le modèle */

proc contents data = &DATA. out = biblio noprint;

run;

proc sql noprint;

select distinct (name) into: list_var separated by » » from biblio where name ne « &Y. »;

quit;

data boosting;

set &DATA.;

/* Initialisation des pondérations */

P = 1/&n.;

run;

%do it = 1 %to &Itefin.;

/* Insérer ici un autre classifieur faible, il faut toutefois que le nouveau cas produise en sortie une table « out », incluant la classification obtenue */

%if &Classifieur. = LOG %then %do;

proc logistic data = boosting noprint;

model &Y. = &list_var.;

weight P;

output out = out predprobs = I;

run;

%end;

/* La dernière itération rajoutée est utilisée uniquement pour produire les prédictions sur les poids finaux */

%if &it. < &Iteration. %then %do;

/* Fusion des données d’origine et des prédictions pour arranger le calcul de l’erreur */

data boosting;

merge boosting out;

Y_hat = 0;

if &Y. = _into_ then Y_hat = 1;

err = P * Y_hat;

run;

/* Calcul de la correction */

proc sql noprint;

select sum(err) into: err from boosting;

quit;

/* Insérer ici d’autre fonction coût */

%if FctCout = Breiman %then %do;

%let err = %sysevalf(0.5 * log(1 – &err.)/&err.);

%end;

/* Propagation de la correction */

data boosting;

set boosting;

P = P * exp(P * Y_hat);

run;

/* Ajustement final des pondérations */

proc sql noprint;

select sum(P) into: err from boosting;

quit;

data boosting;

set boosting;

P = P/&err.;

keep P &Y. &list_var.;

run;

%end;

/* Production des performances en fin d’itération */

proc freq data = out;

tables _from_*_into_;

run;

/* Suppression des tables temporaires et inutiles */

proc datasets lib = work nolist;

delete biblio out;

run;

/* Reset des options d’affichage de la log */

options notes nospool;

%mend;

On applique la macro de la manière suivante :

%Boosting(DATA = E, Y = Y, Classifieur = LOG, FctCout = Breiman, Iteration = 200);

Parmi les éléments à insérer, il faut relever :

– Le tableau sur lequel on veut travailler : $DATA = E$ ;

– Le nom de la réponse à discriminer : $Y = Y$ ;

– Le type de classifieur même si un seul est disponible pour le moment (la régression logistique) : $Classifieur = LOG$ ;

– La fonction coût même si une seule est disponible pour le moment (celle de Breiman) : $FctCout = Breiman$ ;

– Le nombre d’itérations à réaliser : $Iteration = 200$ .

On obtient alors les résultats suivants parmi les tableaux générés en fin de procédure :

, et :

Le premier tableau présente les pondérations finales : $P$ , étant donné que l’on a privilégié sous SAS un classifieur différent de celui utilisé pour les calculs manuels, les résultats ne pourront être comparés.

Le second tableau présente les classifications finales, étant donné que l’on a privilégié sous SAS un classifieur différent de celui utilisé pour les calculs manuels, les résultats ne pourront être comparés. On remarquera alors que si l’on avait utilisé une simple régression logistique, les performances sont de $50 \%$ de bonne classification, contre $70 \%$ selon l’approche boosting.

$\bullet$ Bibliographie :

– The Elements of Statistical Learning de Trevor Hastie, Robert Tibshirani et Jerome Friedman ;

– The top ten algorithms in data mining de Xindong Wu et Vipin Kumar ;

– Probabilité, analyse des données et Statistique de Gilbert Saporta ;

– Data mining et statistique décisionnelle. L’intelligence des données de Stéphane Tufféry.

lemakistatheux

Youhou Mayotte c'est la fête…

Archives de Tag: MARS

Les méthodes de boosting