L’Analyse canonique des corrélations

Harold Hotelling

Historique :

Sommaire :

• Présentation
• L’Analyse canonique des corrélations
• Annexe théorique
• Exemple
• Application sous R
• Application sous SAS
• Bibliographie

Présentation :

L’Analyse canonique des corrélations, élaborée par Harold Hotelling en 1936, est une approche multivariée visant à comparer les interactions de deux matrices et continues. Les deux blocs peuvent être appariés ou non appariés, l’outil étant efficace dans les deux cas.

L’Analyse canonique des corrélations, comme son titre l’indique, se base sur les corrélations, autrement dit sur la présence ou l’absence d’une relation linéaire entre les variables des deux différents blocs.

L’outil appartient à la famille de l’analyse exploratoire et permet, par exemple, de comparer des champs thématiques d’information en élaborant une carte des variables et des observations permettant une représentation visuelle synthétique des interactions entre deux blocs de données.

L’analyse canonique des corrélations :

Hypothèse préliminaire : , continues.

L’Analyse canonique des corrélations se déroule en sept étapes,

– Étape 1 : Centrer-réduire les variables de et   (quoi que non obligatoire mais fortement recommandé).

– Étape 2 : Procéder à la décomposition de Gram-Schimdt () de et . On rappelle qu’une décomposition revient à écrire,

, où , matrices orthogonales et , matrices triangulaires supérieures. On utilisera ensuite la matrice , respectivement , dont le triangle supérieur contient , respectivement , et le reste de la matrice la forme compacte de , respectivement .

– Étape 3 : Extraire la matrice de , et de . Puis faire le produit,

– Étape 4 : Extraire du produit réalisé précédemment les valeurs propres , parts de variance expliquée, et les vecteurs propres associés et qui serviront à boucler les calculs.

– Étape 5 : Calculer les coefficients de corrélation canonique,

– Étape 6 : Calculer les axes factoriels, soit la projection des observations,

– Étape 7 : Projection des variables dans le plan factoriel,

Le choix du nombre d’axes se fait comme pour les autres méthodes d’analyse exploratoire, à partir des valeurs propres et en fonction de leur distribution. Etant donné que l’interprétation est menée analoguement à celle d’une Analyse en Composantes Principales (ACP), alors :

– Plus une variable de l’un des deux blocs est proche du cercle de corrélation et plus elle interagit avec les variables de l’autre bloc ;

– Plus les variables de différents blocs sont proches entre elles et plus leur corrélation est forte, soit que les variables de l’un des deux blocs peuvent s’écrire comme combinaison linéaire à partir des variables de l’autre bloc ;

– Un angle de ° entre deux blocs de variables implique une anti-corrélation entre eux ;

– Un angle de ° entre deux blocs de variables implique l’absence de corrélation entre eux.

Annexe théorique :

On présente ici une esquisse de la démarche méthodologique de l’analyse canonique des corrélations.

Soit muni de la métrique . L’idée est alors de chercher un couple de vecteurs normés sous contrainte d’obtenir l’angle le plus petit et ensuite le couple -orthogonal sous cette même contrainte. On en fait de même pour les autres couples .

Les opérateurs utilisés sont alors de la forme :

,

, dont l’une des propriétés les plus intéressantes est que la restriction de est diagonalisable, de valeurs propres -orthogonales et de vecteurs propres réels positifs.

Cette propriété se démontre facilement par le fait que,

, étant donné que sont -symétriques.

Dés lors, les vecteurs propres , -normés de sont associés aux mêmes valeurs propres. De plus, ils s’expriment comme combinaisons linéaires de et :

, ,

, avec facteurs canoniques obtenus par,

En passant par la formule des matrices de covariance, on en déduit que les équations des facteurs canoniques sont de la forme,

Exemple :

Soit les deux groupes de variables et suivants à comparer,

Dans un premier temps on va centrer-réduire les deux thèmes de variables. On notera alors les résultats : et . Puis on calcule leur décomposition :

On en récupère ensuite les parties orthogonales  : 

, dont le produit donne : 

Pour le calcul des valeurs propres et vecteurs propres associés utiles à la suite des calculs, on procède au développement en valeurs singulières du résultat obtenu précédemment,

, et,

Il va falloir les parties triangulaires pour la suite  : 

Maintenant, on va calculer les coefficients finaux par les deux produits matriciels suivant :  

Ensuite, les projections des observations relatives à et ,

, et,

On peut désormais calculer les coordonnées des variables de et de ,

, que l’on projette dans le plan en deux dimensions (choix motivé par simplicité de lecture étant donné qu’il s’agit d’un exemple),

– Les variables ne sont pas assez proches du cercle de corrélation pour être interprétées.

– Deux groupes sont à relever, le premier concerne les variables soit la possibilité de prédire à partir d’une combinaison linéaire des variables . Le second concerne les variables , soit un lien direct très fort entre elles.

– Les deux groupes décrits ci-dessus sont indépendants étant donné qu’ils forment un angle de °.

– Enfin, la variable est anti-corrélée (angle de °) au premier groupe décrit et indépendante au second (angle de °).

Application sous R :

Soit l’exemple suivant :

E = data.frame(X1 = c(0.8970, 2.0949, 3.0307, 4.0135, 5.0515, 6.0261, 6.9059, 7.9838, 8.9854, 9.9468), X2 = c(8.1472, 9.0579, 1.2699, 9.1338, 6.3236, 0.9754, 2.7850, 5.4688, 9.5751, 9.6489), X3 = c(3.1101, 4.1008, 4.7876, 7.0677, 6.0858, 4.9309, 4.0449, 3.0101, 5.9495, 6.8729), X4 = c(1.9593, 2.5472, 3.1386, 4.1493, 5.2575, 9.3500, 10.1966, 11.2511, 9.6160, 10.4733), X5 = c(11.1682, 11.9124, 12.9516, 13.9288, 14.8826, 15.9808, 16.9726, 18.1530, 18.9751, 19.8936), X6 = c(1.5761, 9.7059, 9.5717, 4.8538, 8.0028, 1.4189, 4.2176, 9.1574, 7.9221, 9.5949), X7 = c(1.0898, 1.9868, 2.9853, 10.0080, 8.9052, 8.0411, 2.0826, 1.0536, 9.0649, 10.0826), X8 = c(16.8407, 17.2543, 18.8143, 19.2435, 20.9293, 11.3517, 9.8308, 10.5853, 11.5497, 9.9172))

Package et fonction R : https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/cancor

La fonction cancor du package candisc permet de réaliser l’analyse canonique des corrélations. Après chargement de la librairie, on procède de la manière suivante :

cancor(x = E[,c(« X1 », « X2 », « X3 », « X4 »)], y = E[,c(« X5 », « X6 », « X7 », « X8 »)], xcenter = TRUE, xscale = TRUE, ycenter = TRUE, yscale = TRUE)

Parmi les éléments à insérer les plus importants il faut relever :

–  La première matrice de données thématiques : ;

–  La première matrice de données thématiques : ;

– Le fait de centrer-réduire le premier jeu de données : ;

– Le fait de centrer le second jeu de données : .

On obtient alors les résultats suivants :

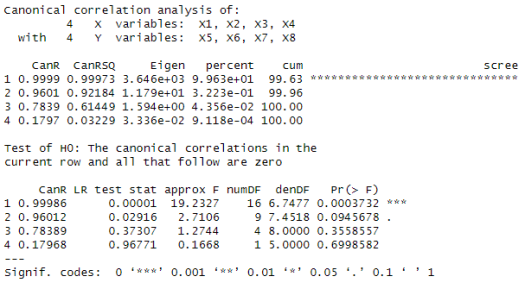
, qui ne sont pas forcément les plus utiles, toutefois,

– On retrouve dans la colonne les valeurs propres, qui sont les mêmes que celles obtenues lors des calculs manuels (cf partie « Exemple ») ;

– L’application de la fonction sur l’objet créé permet d’afficher les coefficients canoniques, qui diffèrent de ceux obtenus par les calculs manuels (cf partie « Exemple ») non pas par l’algorithme utilisé mais par la façon de centrer-réduire les données ;

– Les coordonnées de projection des variables selon le plan voulu : , qui sont les mêmes que celles obtenues lors des calculs manuels (cf partie « Exemple »).

Application sous SAS :

Soit l’exemple suivant :

data E;
input Obs X1 X2 X4 X5 X6 X7 X8;
cards;
0.8970 8.1472 3.1101 1.9593 11.1682 1.5761 1.0898 16.8407
2.0949 9.0579 4.1008 2.5472 11.9124 9.7059 1.9868 17.2543
3.0307 1.2699 4.7876 3.1386 12.9516 9.5717 2.9853 18.8143
4.0135 9.1338 7.0677 4.1493 13.9288 4.8538 10.0080 19.2435
5.0515 6.3236 6.0858 5.2575 14.8826 8.0028 8.9052 20.9293
6.0261 0.9754 4.9309 9.3500 15.9808 1.4189 8.0411 11.3517
6.9059 2.7850 4.0449 10.1966 16.9726 4.2176 2.0826 9.8308
7.9838 5.4688 3.0101 11.2511 18.1530 9.1574 1.0536 10.5853
8.9854 9.5751 5.9495 9.6160 18.9751 7.9221 9.0649 11.5497
9.9468 9.6489 6.8729 10.4733 19.8936 9.5949 10.0826 9.9172
;
run;

Procédure SAS: https://support.sas.com/documentation/cdl/en/statug/63033/HTML/default/statug_cancorr_sect005.htm

La procédure CANCOR de SAS permet de réaliser l’analyse canonique des corrélations. On procède de la manière suivante :

proc cancorr data = E;
var X1 X2 X3 X4;
with X5 X6 X7 X8;
ods exclude MultStat StdCanCoefV StdCanCoefW;
run;

Parmi les éléments à insérer les plus importants il faut relever :

– La base de données où trouver les variables : ;

–  Les variables du premier thème : ;

–  Les variable du second thème : ;

– L’ODS exclude est utilisé pour supprimer les sorties sans intérêt.

On obtient alors les résultats suivants :

On vérifie,

– Le premier tableau (coupé en deux pour la mise en page) contient les valeurs propres, qui sont les mêmes que celles obtenues lors des calculs manuels (cf partie « Exemple ») ;

– Les deuxième et troisième tableaux (« Coefficients canoniques bruts. pour le/la Variables VAR/WITH ») contiennent les composantes et associée aux valeurs propres du premier tableau, qui diffèrent de celles obtenues lors des calculs manuels (cf partie « Exemple ») non pas par l’algorithme utilisé mais par la méthode pour centrer-réduire les données ;

– Les quatrième et cinquième tableaux (« Corrélation entre le(la) Variables VAR/WITH et leurs composantes canoniques ») contiennent les coordonnées des variables dans le plan factoriel, qui sont les mêmes que celles obtenues lors des calculs manuels (cf partie « Exemple »).

Bibliographie :

– Relations Between Two sets of Variates de Harold Hotelling ;

– Probabilités, analyse des données et Statistique de Gilbert Saporta ;

– Data mining et statistique décisionnelle. L’intelligence des données de Stéphane Tufféry ;

– Comprendre et utiliser les statistiques dans les sciences de la vie de Bruno Falissard ;

– Analyses factorielles simples et multiples de Brigitte Escofier et Jérôme Pagès ;

– La présentation powerpoint: http://iml.univ-mrs.fr/~reboul/canonique.pptx.pdf