Les modèles épidémiologiques

De gauche à droite : Daniel Bernoulli, Ronald Ross, William Ogilvy Kermack, Anderson Gray McKendrik et Richard Doll

Historique :

Sommaire :

• Présentation
• Les modèles épidémiologiques
  • Du modèle au modèle
  • Le compartiment et le modèle
  • Le modèle métapopulationnel
  • Les effets naissances, migrations et décès naturels
  • Quelques autres compartiments classiques
  • Le nombre de reproduction effectif
• Annexe théorique
  • Les Equations Différentielles Ordinaires
  • L’Algorithme d’Euler
  • L’Algorithme de Runge-Kutta
• Exemple
  • Le modèle
  • Le modèle métapopulationnel
• Application sous R
• Application sous SAS
• Bibliographie

Présentation :

Les modèles compartimentaux épidémiologiques sont une famille d’outils d’anticipation et de compréhension des dynamiques de propagation des maladies, jouant un rôle central dans le domaine de la Santé publique. Ils ont fait énormément parler d’eux au cours de la crise Covid-19 mondiale traversée de 2020 à 2022. Leur principe consiste à s’appuyer sur une liste de paramétrages contextuels pour ensuite proposer une série de projections sur un nombre fixé de temps.

Les modèles épidémiologiques ont évolué au fil du temps grâce aux contributions de nombreux chercheurs, mathématiciens et épidémiologistes. Néanmoins, certaines figures clés ont marqué des étapes cruciales dans leur développement. On pourra citer Daniel Bernoulli qui, au XVIIIème siècle, a jeté les bases de la modélisation des phénomènes aléatoires, élément clé des modèles épidémiologiques. Bases qui ont été ensuite développées par Ronald Ross en contribuant à la modélisation mathématique des maladies infectieuses, notamment le paludisme, éclairant la compréhension de sa transmission par les vecteurs. Parmi les autres célébrités à évoquer, et cet article pêchera dans l’exhaustivité de cette liste, on peut également parler de William Ogilvy Kermack et d’Anderson Gray McKendrick qui, en 1927, publient un article fondateur introduisant le modèle précurseur des modèles épidémiologiques complexes modernes. Enfin, deux dernières personnalités emblématiques : Richard Doll et Austin Bradford Hill, qui ont joué un rôle important dans la formalisation des études épidémiologiques et notamment établi les principes cruciaux sur la causalité entre des facteurs spécifiques et des maladies.

Ces outils se basent sur la notion de système d’Equations Différentiels Ordinaires (EDO) et de leur résolution afin de déterminer à chaque itération les différents volumes associés aux compartiments considérés, permettant alors à tracer la courbe d’évolution de l’épidémie selon autant d’angles qu’il y a de compartiments.

Les modèles épidémiologiques :

Hypothèse préliminaire : Un jeu de paramètres en adéquation avec les différents compartiments utilisés.

– Du modèle au modèle

Il faut définir au préalable une unité de temps : , et son maximum : . De cette manière, on fixe déjà la temporalité  sur laquelle la modélisation sera réalisée. Enfin, on note la somme des effectifs de tous les compartiments utilisés, soit la population total étudiée.

Il y a deux compartiments classiques dans les modèles épidémiologiques : le pour « Susceptibles », soit les susceptibles d’être contaminés car sains, et il ne faut pas confondre un individu sain avec un individu immunisé. Le pour « Infectés », soit les individus sains qui ont fini par être contaminés. On fixe alors le paramètre , probabilité qu’un individu fasse la transition : à chaque instant . Ces deux premiers compartiments forment à eux-seuls le modèle , regroupant de façon simpliste l’ensemble des infections virales chroniques n’ayant aucune incidence sur la mortalité (on pourra citer par exemple l’herpès simplex dont on ne meurt et ne guérit pas). On peut exprimer les volumes/effectifs à l’instant au sein de chacun de ces deux compartiments sous la forme généralisée :

, à ce stade les paramètres sont supposés nuls, on y reviendra plus tard. On définit alors les états initiaux : , et on érige le système sous la forme du système d’Equations Différentielles à résoudre suivant :

A noter que l’un des indicateurs phares utilisés pour le suivi des épidémies est celui du nombre ou incidence de nouveaux cas. On peut l’obtenir alors très facilement en l’extrayant de la formule, et de forme :

On enrichit le modèle en introduisant maintenant la notion de guérison grâce au compartiment . Dès lors, on passe du phénomène assez rare d’infections virales chroniques sans réelle conséquence à n’importe quelles maladies dont on guérit mais ne meurt pas, spectre particulièrement large et dont on pourrait citer le rhume en guise d’exemple. L’ajout de ce compartiment se fait avec celui du paramètre traduisant mathématiquement le taux de guérison. Le volume/effectif associé au compartiment à l’instant est alors :

A noter que l’insertion de ce nouveau compartiment a également une incidence sur le compartiment comme on peut le voir sur l’intégrale généralisée décrite précédemment. On définit alors les états initiaux : , et on érige le système sous la forme du système d’Equations Différentielles à résoudre suivant :

Enfin, on rajoute maintenant un dernier compartiment relatif aux décès : . Il s’agit des personnes infectées par la maladie et qui en sont décédées. Ces modèles permettent ainsi d’intégrer toute maladie à risque endémique avec un potentiel risque de mortalité. Sa mise en place s’accompagne de l’ajout du paramètre retranscrivant le taux de mortalité. Le volume/effectif associé à ce compartiment et à l’instant est alors :

Tout comme pour le compartiment , l’insertion du compartiment a également une incidence sur le compartiment comme on peut le voir sur l’intégrale généralisée décrite précédemment. On définit alors les états initiaux : , et on érige le système sous la forme du système d’Equations Différentielles à résoudre suivant :

– Le compartiment et le modèle

Le principal défaut que l’on peut trouver au modèle , outre sa simplicité, est de ne pas prendre en compte le principe d’incubation d’une maladie. Il s’agit plus particulièrement du temps écoulé entre la contamination et le début des symptômes, soit, d’une certaine manière, la longueur de la flèche : . Ce qui vaut à ce principe un compartiment à part entière et noté : , c’est qu’en plus de créer un décalage dans le temps de la propagation du virus étudié, il permet de prendre en compte le stade de progression de la maladie chez un individu infecté qui, méconnaissant son statut réel pourra en contaminer d’autres qui sont sains et sans s’en rendre compte. Dès lors, le terme d’Exposés est utilisé. Cet enrichissement permet aux modèles épidémiologiques de s’approcher toujours un peu plus des mécanismes des maladies à risque endémique et modifie sensiblement la forme généralisée du volume/effectif associée au compartiment du fait de liaison imbriquée :

, en définissant le nouveau paramètre

On fixe les états initiaux : , et on érige le système sous la forme du système d’Equations Différentielles à résoudre suivant :

– Le modèle métapopulationnel

Une manière d’améliorer le modèle construit est d’intégrer dans son schéma d’Equations Différentielles l’information sur le taux de contact entre les différentes classes d’âge d’une population. Par exemple, si l’on suppose que l’épidémie que l’on cherche à modéliser se déroule dans un pays avec un moyenne d’âge particulièrement jeune, ajouter un paramètre qui permettra de pondérer le taux de transmission en fonction du taux de contact inter-classe d’âge pourra apporter un boost de précision très intéressant.

On doit donc définir ce l’on appelle une matrice de contacts de forme symétrique suivante :

, avec les différentes classes ou intervalles d’âge paramétrés et le taux de contact entre les classes d’âge et . Le modèle épidémiologique s’en voit fortement enrichi puisqu’il intègre dans son concept les probabilités de transiter d’une classe d’âge à l’autre. Si l’on prend par exemple le modèle , on intègre ce concept ainsi :

, avec et des vecteurs de taille des volumes ventilés par classe d’âge.

– Les effets naissances, migrations et décès naturels

Les modèles vus précédemment sont plus souvent utilisés pour les épidémies ponctuelles et sont d’ailleurs assez flexibles pour procéder à des réajustements lors d’une propagation en cours ou même établir des scénarios servant à modéliser plusieurs vagues successives. Pour cela il suffit simplement d’adapter les paramètres initiaux à la situation rencontrée. A partir du moment où l’objectif devient la modélisation d’un phénomène s’allongeant dans le temps, il est important d’intégrer dans son modèle les notions de :

• Nouvelles naissances, qui implique que la population croît régulièrement sur un profil bien spécifique venant ainsi alimenter uniquement le compartiment . Cet effet sera noté ;
• Effets migratoires, avec une perte ou un gain de population. Les notions de cas importés et autochtones prennent tout leur sens, et de fait, venant alimenter tous les compartiments. Cet effet sera noté ;
• Décès naturels, à ne pas confondre avec les décès du compartiment directement liés à la maladie modélisée, et donc de diminution de la population, touchant alors tous les compartiments également. Cet effet sera noté .

Si l’on souhaite enrichir à nouveau le modèle vu précédemment, cela donne, pour les états initiaux :

– Quelques autres compartiments classiques

Enfin, il est possible de rajouter pléthore de compartiments différents et variés dans l’objectif de coller au mieux au contexte : 

• Le compartiment des vaccinés, noté , intégrant à la fois le taux de vaccinés de départ et celui de nouveaux vaccinés ;
• Le compartiment des mis en quarantaine, noté , intégrant le taux de mis en quarantaine, de guéris et de décès en quarantaine ;
• Le compartiment des asymptomatiques, noté , intégrant le taux d’infectieux asymptomatiques qui présentent un enjeu important lors du contrôle d’une épidémie du fait qu’ils sont capables d’infecter d’autres porteurs sains et quasi-impossible à repérer ;
• Le compartiment des immunisés après infection et guérison, noté , et son taux associé ;
• Le second compartiment qui permet de remettre en jeu les individus infectés, guéris et non immunisés dans le premier compartiment , et son taux associé.

– Le nombre de reproduction de base

Le ou « Nombre de Reproduction de Base » est une mesure cruciale en épidémiologie, offrant des indications sur la transmission d’une maladie dans une population (à ne pas confondre avec le volume/effectif d’individus du compartiment , des guéris, à l’instant initial ). Il s’agit du nombre moyen d’infections secondaires résultant d’un individu infecté introduit dans une population totalement susceptible. Autrement dit, il mesure la capacité d’une maladie à se propager à travers une population. Son calcul est dépendant du type de modèle utilisé. En reprenant les notations précédentes, en voici plusieurs de ses formes :

– Pour le modèle , ;

– Pour le modèle , ;

– Pour les modèles , et , ;

– Pour le modèle , ;

– Pour le modèle , .

Il est également possible de déterminer le nombre moyen de nouvelles infections à un instant et noté (nombre de reproduction effectif instantané). Sa formule, quel que soit la forme du modèle est :

La différence essentielle entre et est en fait liée à son objectif d’utilisation. Par exemple, pour qualifier une maladie spécifique, le apportera une information sur sa vitesse de propagation globale permettant de caractériser son niveau de dangerosité. Alors que le trouve son intérêt dans le suivi d’une épidémie en tant qu’indicateur synthétisant son stade d’évolution, souvent utilisé en Santé publique afin déterminer la dimension des mesures de contrôle à mettre en œuvre.

En termes de lecture, un correspond à une épidémie en pleine propagation puisqu’un individu infecté en contamine au moins un, lorsqu’elle stagne avec un infecté qui contamine un seul sain, et pour son déclin, un infecté en contamine moins d’un.

A noter que les formules du et du reposent sur des hypothèses simplificatrices, telles que l’homogénéité de la population et la constance des paramètres. Dans des contextes plus complexes, où ces conditions ne sont pas remplies, des ajustements et des modèles plus élaborés peuvent être nécessaires pour les évaluer.

Annexe théorique :

– Les équations différentielles ordinaires

Les modèles épidémiologiques à compartiments se basent sur la notion de système d’Equations Différentielles Ordinaires (EDO). Pour obtenir une prévision à un instant , on résout ce système donnant les différents volumes associés aux différents compartiments. Une EDO à l’ordre est de la forme générale : 

, avec fonction adaptée à la forme des compartiments que l’on veut considérer dans le modèle et de forme : 

Les EDO disposent de plusieurs propriétés essentielles et offrant aux modèles épidémiologiques compartimentaux des caractéristiques des plus pratiques :

– Le théorème d’existence et d’unicité de Picard-Lindelöf et de Cauchy-Lipschitz permet aux EDO, sous certaines conditions, d’admettre une solution qui existe et est unique, relativement aux conditions initiales données ;

Théorème : Soit une équation différentielle ordinaire du premier ordre avec la condition initiale , où est continue dans une région rectangulaire et . Si est Lipschitz continue par rapport à dans , c’est-à-dire qu’il existe une constante telle que pour tous et dans , alors l’EDO a une unique solution dans un intervalle , où est le plus petit des nombres et .

– De ce théorème découle également le concept d’EDO autonome, assurant son indépendance en fonction du temps. Cela signifie que les taux de variation des variables dépendent uniquement des valeurs actuelles des variables, et non du temps ;

– Le critère de stabilité de Nyquist et le critère de Hurwitz assure la stabilité linéaire pour les systèmes dynamiques décrits par des EDO. Pour les solutions non linéaires, c’est le théorème de stabilité de Lyapunov qui joue un rôle fondamentale. La notion de stabilité indique comment les solutions réagissent aux petites perturbations des conditions initiales ;

Définition : Soit un système dynamique décrit par l’équation différentielle alors le critère de stabilité de Nyquist s’applique à un système linéaire sous la forme de fonction de transfert déterminé par,

1. avec variable de Laplace.
2. Elle admet des valeurs spécifiques de sur le plan complexe le long de l’axe imaginaire , unité imaginaire et fréquence angulaire.
3. Après tracé de la fonction , on peut conclure en la stabilité du système si et seulement si la courbe ne contourne pas le point critique .

Définition : Soit un système dynamique décrit par l’équation différentielle alors le critère de stabilité de Hurwitz s’applique à un système polynomial déterminé par,

1. L’équation : .
2. On détermine la matrice de Hurwitz associée aux coefficients de cette équation.
3. On peut conclure en la stabilité du système si et seulement tous les mineurs principaux, ou déterminants associés aux sous-matrices, sont strictement positifs.

Définition : Soit un domaine contenant l’équilibre d’un système dynamique décrit par l’équation différentielle : , où est un vecteur d’état dans est une fonction continue, et est un point d’équilibre tel que .

Supposons qu’il existe une fonction continue définie positive, c’est-à-dire que , avec . De plus, considérons une fonction définie sur telle que sa dérivée le long des trajectoires du système soit semi-définie négative, c’est-à-dire .

Alors, l’équilibre est stable au sein de Lyapunov. Si, de plus, , alors l’équilibre est asymptotiquement stable au sens de Lyapunov. En d’autres termes, la fonction est une fonction Lyapunov candidate, et la dérivée joue le rôle d’une mesure de la stabilité du système. Si est toujours négative (ou nulle), cela indique que le système est stable ou asymptotiquement stable, respectivement, autour de l’équilibre .

Ces caractéristiques des EDO font qu’elles sont couramment utilisées pour modéliser les systèmes dynamiques. Ces systèmes peuvent représenter divers phénomènes, tels que la croissance de la population, les mouvements planétaires, les réactions chimiques, etc. On peut les résoudre selon deux principales méthodes : l’algorithme de Newton et l’algorithme de Runge-Kutta.

– L’Algorithme d’Euler

L’algorithme d’Euler est une méthode itérative numérique, proposée par Leonhard Euler au XVIIIème siècle, utilisée pour résoudre des équations différentielles ordinaires. Dans le contexte des modèles épidémiologiques, cette méthode peut être appliquée pour résoudre des systèmes d’équations différentielles non linéaires, généralement associés à des modèles plus complexes. C’est une méthode itérative qui se base sur le principe que, près d’une solution, une fonction peut être approximée par une droite tangente à la courbe. Les itérations successives conduisent à une convergence rapide vers la solution.

Étapes de l’algorithme,

1. Initialisation : Définir une équation différentielle , un pas de temps et une condition initiale ;
2. Itérations :
   • ;
   • Avec , une estimation de , et est la dérivée de par rapport à évaluée en .
3. Répéter l’étape deux jusqu’à atteindre la fin de l’intervalle temporel spécifié.

– L’Algorithme de Runge-Kutta

L’algorithme de Runge-Kutta, développé par les mathématiciens allemands Carl Runge et Martin Kutta au début du XXe siècle, constitue une avancée significative dans la résolution numérique d’EDO. Leur objectif était d’améliorer la méthode d’Euler, en proposant une approche plus précise et stable pour approximer les solutions d’EDO. Les méthodes numériques Runge-Kutta, notamment celle d’ordre () sont aujourd’hui les plus largement utilisées pour résoudre une variété de problèmes scientifiques, y compris les modèles mathématiques en épidémiologie, en offrant un bon compromis entre précision et complexité. Cet algorithme utilise des coefficients pour pondérer les pentes de la fonction à différents points le long du pas de temps. L’itération est répétée jusqu’à ce que la solution soit calculée sur tout l’intervalle temporel souhaité.

Étapes de l’algorithme,

1. Initialisation : Définir une équation différentielle , un pas de temps et une condition initiale ;
2. Itération :
   • Calculer les coefficients intermédiaires , et comme suit,
     • ;
       
     • ;
     • ;
     • .
   • Mettre à jour la solution ;
   • Mettre à jour le temps : ;
3. Répéter l’étape deux jusqu’à atteindre la fin de l’intervalle temporel spécifié.

Exemple :

Le modèle

On cherche à modéliser la propagation d’une maladie sur un territoire selon un modèle qui correspond parfaitement aux attentes puisque l’on dispose des paramètres associés. Ainsi, on définit le taux de contamination , avec une durée d’incubation de « temps » le taux d’incubation , le taux de guérison et le taux de décès associé à , . On veut que ce modèle donne des prévisions sur « temps » avec un pas .

Enfin, on initialise la modélisation avec individus sains, infecté introduit dans la population concernée et dont les symptômes ne sont pas encore apparus (« exposé »), infecté avec symptômes, guéri et décédé par la pathologie . Soit un effectif total . 

Ainsi, pour ,

, avec à ce temps, un nombre de nouveaux cas de :

Pour ,

, avec à ce temps, un nombre de nouveaux cas de :

Pour ,

, avec à ce temps, un nombre de nouveaux cas de :

On continue les calculs jusqu’à avoir parcouru tous les temps . Et si l’on affiche le graphe que l’on obtient avec les différents vecteurs associés à chacun des compartiments alors on obtient la figure suivante :

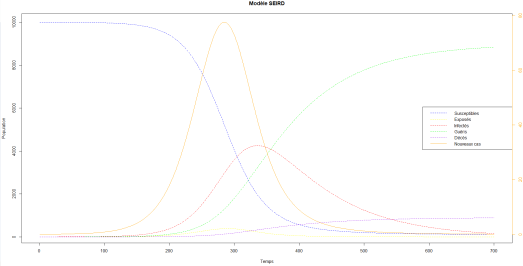
A la fin de cette vague, on extrait les indicateurs de Santé publique associés à l’épidémie de la maladie suite à son introduction au sein de la population que l’on observe :

– individus ont été infectés, soit  de la population totale ;

– individus en sont décédés, soit de la population totale ;

– Le pic de l’épidémie a eu lieu à avec nouveaux cas à ce temps-là.

Le modèle métapopulationnel

On cherche à modéliser la propagation d’une maladie sur un territoire selon un modèle qui correspond parfaitement aux attentes puisque l’on dispose des paramètres associés. Ainsi, on définit le taux de contamination , avec une durée d’incubation de « temps » le taux d’incubation , le taux de guérison et le taux de décès associé à , . On veut que ce modèle donne des prévisions sur « temps » avec un pas .

On inclut également la matrice de contacts entre les différentes classes d’âge que l’on a à disposition. Ces classes d’âge sont construites selon un découpage en cinq intervalles de même longueur :

Enfin, on initialise la modélisation avec individus sains pour les différentes classes d’âge, infecté, de 0-20 ans, introduit dans la population concernée et dont les symptômes ne sont pas encore apparus (« exposé »), infecté avec symptômes, guéri et décédé par la pathologie .

Soit un effectif total,

Ainsi, pour ,

, avec à ce temps, un nombre de nouveaux cas par classe d’âge de :

Pour ,

, avec à ce temps, un nombre de nouveaux cas par classe d’âge de :

Pour ,

, avec à ce temps, un nombre de nouveaux cas par classe d’âge de :

On continue les calculs jusqu’à avoir parcouru tous les temps . Et si l’on affiche le graphe que l’on obtient avec les différents vecteurs associés à chacun des compartiments  et sommés sur les effectifs ventilés par classe d’âge à chaque instant , alors on obtient la figure suivante :

A la fin de cette vague, on extrait les indicateurs de Santé publique associés à l’épidémie de la maladie suite à son introduction au sein de la population que l’on observe :

– individus ont été infectés, soit  de la population totale ;

– individus en sont décédés, soit de la population totale ;

– Le pic de l’épidémie a eu lieu à avec nouveaux cas à ce temps-là.

[latex]\bullet[/latex] Application sous R :

On proposera la fonction suivante permettant de produire des modélisations incluant les compartiments  :

Model_epidemiologique = function(S0,E0,I0,R0,D0,beta,sigma,gamma,delta,pas,T) {

# La fonction s’adapte en fonction du paramétrage rentré. S0 correspond au volume d’individus susceptibles/sains de départ associé à beta le taux de contamination (si <= 0 alors le fonction ne se lance pas), E0 à celui d’exposés/contaminés n’ayant pas encore développé les symptômes associé à sigma le taux d’incubation (si <= 0 alors le compartiment est exclu), I0 à celui d’infectés, R0 à celui des guéris associé à gamma le temps de guérison (si <= 0 alors le compartiment est exclu) et D0 à celui des décédés suite à la pathologie étudiée associé à delta le taux de mortalité lié à la pathologie (si <= 0 alors le compartiment est exclu). Les paramètres pas et T représentant respectivement l’unité de temps et le nombre de temps total parcouru.  

Model_epidemiologique = function(S0,E0,I0,R0,D0,beta,sigma,gamma,delta,pas,T) {

# Si l’on ne veut pas utiliser le compartiment E, et comme l’erreur est facile, on applique un réajustement ici si on s’est trompé
if (sigma == 0 && I0 == 0 && E0 > 0) {
print(« Attention, le paramètre sigma étant nul, le compartiment E ne sera pas utilisé, or sur votre paramétrage Sigma = 0, E > 0 et I = 0, aussi le programme va intervertir les valeurs de E et I »)
I0 = E0
E0 = 0
}

# Chargement de la bibliothèque pour la résolution d’équations différentielles
library(deSolve)

# Fonction générique du modèle SEIRD avec tous les compartiments voulus pour cette fonction
seird_model <- function(t, y, parameters) {
with(as.list(c(y, parameters)), {
dS = (-beta * S * I / N) * pas
if (sigma > 0) {
dE = (beta * S * I / N – sigma * E) * pas
dI = (sigma * E – (gamma + delta) * I) * pas
}
if (sigma == 0) {
dE = 0
dI = (beta * S * I/N – gamma * I) * pas
}
dR = (gamma * I) * pas
dD = (delta * I) * pas
return(list(c(dS, dE, dI, dR, dD)))
})
}

# Conditions initiales
initial_conditions = c(S = S0, E = E0, I = I0, R = R0, D = D0)

# Création du vecteur des différents temps
times = seq(0, T, by = pas)

# Auto-configuration des paramètres du modèle pour l’utilisation de la fonction ode du package deSolve
NAME = « S »
CHOIX = « S »
initiale_state = 1
LEGEND = « Susceptibles »
COL = « blue »
parameters = c(beta = beta)
if (sigma > 0) {
NAME = paste(NAME, « E »)
CHOIX = c(CHOIX, »E »)
LEGEND = c(LEGEND, « Exposés »)
COL = c(COL, « yellow »)
parameters = c(parameters, sigma = sigma)
}
if (beta > 0) {
NAME = paste(NAME, « I »)
CHOIX = c(CHOIX, »I »)
LEGEND = c(LEGEND, « Infectés »)
COL = c(COL, « red »)
}
if (gamma > 0) {
NAME = paste(NAME, « R »)
CHOIX = c(CHOIX, »R »)
LEGEND = c(LEGEND, « Guéris »)
COL = c(COL, « green »)
parameters = c(parameters, gamma = gamma)
}
if (delta > 0) {
NAME = paste(NAME, « D »)
CHOIX = c(CHOIX, »D »)
LEGEND = c(LEGEND, « Décès »)
COL = c(COL, « purple »)
parameters = c(parameters, delta = delta)
}

# Calcul de la population totale pour application des équations différentielles
N = S0 + E0 + I0 + R0 + D0
parameters = c(parameters, pas = pas, N = N)

# Si le paramètre beta est différent de 0 alors on peut lancer la modélisation, si ce dernier est égal à 0, au regard de la formule des équations différentielles, assez logiquement on ne peut lancer les calculs
if (beta > 0) {
# Résolution des équations différentielles avec la fonction ode
result = ode(y = initial_conditions, times = times, func = seird_model, parms = parameters)
# Sélection des colonnes d’intérêt en fonction du type de modèle décrit par les paramètres entrés
result = result[,c(« time »,CHOIX)]

# Tracé des résultats
plot(times, result[, « S »], type = « l », lty = 1, col = « blue », xlab = « Jours », ylab = « Population », main = NAME, ylim = c(0,N))
for (p in 3:dim(result)[2]) {lines(times, result[, CHOIX[p-1]], lty = 1, col = COL[p – 1])}
legend(« topright », legend = LEGEND, col = COL, lty = 1)
}

if (beta == 0) {print(« A minima, le paramètre Beta doit être > 0 »)}
}

On souhaite lancer la modélisation d’un . Pour cela on procède de la manière suivante :

Model_epidemiologique(S0=9999,E0=1,I0=0,R0=0,D0=0,beta=0.05,sigma=0.2,gamma=0.01,delta=0.001,pas=1,T=1000)

Parmi les éléments à insérer les plus importants il faut relever :

–  Le volume de susceptibles de départ : ;

–  Le volume d’exposés de départ : ;

–  Le volume d’infectés de départ : ;

–  Le volume de guéris de départ : ;

–  Le volume de décédés de départ : ;

–  Le taux de contamination : ;

–  Le taux d’incubation : ;

–  Le taux de guérison : ;

–  Le taux de décès : .

On obtient alors les résultats suivants :

, qui sont alors les mêmes que ceux obtenus lors des calculs manuels (cf partie « Exemple »).

Application sous SAS :

On proposera la macro suivante permettant de produire des modélisations incluant les compartiments  :

%macro Model_epidemiologique(S0=, E0=, I0=, R0=, D0=, beta=, sigma=, gamma=, delta=, pas=, T=);

/* La fonction s’adapte en fonction du paramétrage rentré. S0 correspond au volume d’individus susceptibles/sains de départ associé à beta le taux de contamination (si <= 0 alors le fonction ne se lance pas), E0 à celui d’exposés/contaminés n’ayant pas encore développé les symptômes associé à sigma le taux d’incubation (si <= 0 alors le compartiment est exclu), I0 à celui d’infectés, R0 à celui des guéris associé à gamma le temps de guérison (si <= 0 alors le compartiment est exclu) et D0 à celui des décédés suite à la pathologie étudiée associé à delta le taux de mortalité lié à la pathologie (si <= 0 alors le compartiment est exclu). Les paramètres pas et T représentant respectivement l’unité de temps et le nombre de temps total parcouru. */

options nonotes;

%if &beta. > 0 %then %do;

/* Si l’on ne veut pas utiliser le compartiment E, et comme l’erreur est facile, on applique un réajustement ici si on s’est trompé */

%if (&sigma. = 0 and &I0. = 0 and &E0. > 0) %then %do;

%put Attention, le paramètre sigma étant nul, le compartiment E ne sera pas utilisé, or sur votre paramétrage Sigma = 0, E > 0 et I = 0, aussi le programme va intervertir les valeurs de E et I;

%let I0 = &E0.;

%let E0 = 0;

%end;

/* Initialisation des compartiements */

%let N = %sysevalf(&S0. + &E0. + &I0. + &R0. + &D0.);

%let S = &S0.;

%let E = &E0.;

%let I = &I0.;

%let R = &R0.;

%let D = &D0.;

data Modelisation;

t = 0;

S = &S0.; E = &E0.; I = &I0.; R = &R0.; D = &D0.;

dS = 0; dE = 0; dI = 0; dR = 0; dD = 0;

N = &N.;

run;

/* Algorithme de calcul des différents compartiments à chaque instant t */

%do t = 1 %to &T.;

%put &t.;

/* Compartiment Susceptibles */

%let dS = %sysevalf(-(&beta. * &S. * &I. / &N.) * &pas.);

/* Compartiment Exposés & Infectés */

%if &sigma. > 0 %then %do;

%let dE = %sysevalf((&beta. * &S. * &I. / &N. – &sigma. * &E.) * &pas.);

%let dI = %sysevalf((&sigma. * &E. – (&gamma. + &delta.) * &I.) * &pas.);

%end;

/* Version du compartiment Infectés si celui Exposés n’est pas enclenché */

%if &sigma. = 0 %then %do;

%let dE = 0;

%let dI = %sysevalf((&beta. * &S. * &I./&N. – &gamma. * &I.) * &pas.);

%end;

/* Compartiment Guéris */

%let dR = %sysevalf((&gamma. * &I.) * &pas.);

/* Compartiment Décès */

%let dD = %sysevalf((&delta. * &I.) * &pas.);

/* Mise à jour des compartiements */

%let S = %sysevalf(&S. + &dS.);

%let E = %sysevalf(&E. + &dE.);

%let I = %sysevalf(&I. + &dI.);

%let R = %sysevalf(&R. + &dR.);

%let D = %sysevalf(&D. + &dD.);

data ajout;

t = &t.;

S = &S.; E = &E.; I = &I.; R = &R.; D = &D.;

dS = &dS.; dE = &dE.; dI = &dI.; dR = &dR.; dD = &dD.;

N = S + E + I + R + D;

run;

data Modelisation;

set Modelisation ajout;

run;

%end;

/* Tracé des résultats */

proc sgplot data=Modelisation;

series x = t y = S / legendlabel = « Susceptibles » lineattrs = (color = blue);

%if &sigma. > 0 %then %do;

series x = t y = E / legendlabel = « Exposés » lineattrs = (color = yellow);

%end;

series x = t y = I / legendlabel = « Infectés » lineattrs = (color = red);

%if &gamma. > 0 %then %do;

series x = t y = R / legendlabel = « Rétablis » lineattrs = (color = green);

%end;

%if &delta. > 0 %then %do;

series x = t y = D / legendlabel = « Décès » lineattrs = (color = purple);

%end;

xaxis label = « Temps »;

yaxis label = « Population »;

keylegend / location = inside position = topright;

run;

%end;

%if &beta. = 0 %then %do;

%put Beta doit être supérieur à 0;

%end;

options notes;

%mend;

On souhaite lancer la modélisation d’un . Pour cela on procède de la manière suivante :

%Model_epidemiologique(S0=9999, E0=1, I0=0, R0=0, D0=0, beta=0.05, sigma=0.2, gamma=0.01, delta=0.001, pas=1, T=100);

Parmi les éléments à insérer les plus importants il faut relever :

–  Le volume de susceptibles de départ : ;

–  Le volume d’exposés de départ : ;

–  Le volume d’infectés de départ : ;

–  Le volume de guéris de départ : ;

–  Le volume de décédés de départ : ;

–  Le taux de contamination : ;

–  Le taux d’incubation : ;

–  Le taux de guérison : ;

–  Le taux de décès : .

On obtient alors les résultats suivants :

, qui sont alors les mêmes que ceux obtenus lors des calculs manuels (cf partie « Exemple »).

Bibliographie :

– A contribution to the mathematical theory of epidemics de W. O. Kermack et A. G. McKendrick ; 

– Infectious diseases of humans : Dynamics and control de R. M. Anderson et R. M. May ;

–  On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations de O. Diekmann, J. A. Heesterbeek et J. A. Metz ;

– The mathematics of infectious diseases de H. W. Hethcote ; 

–  Modeling infectious diseases in humans and animals de M. J. .Keeling et P. Rohani ;

– Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission de P. Van den Driessche et J.  Watmough ; 

– Appropriate models for the management of infectious diseasesde H. J. Wearing, P. Rohani et M. J. Keeling ; 

– Le site web : https://images.math.cnrs.fr/Modelisation-d-une-epidemie-partie-1.html ;

– Simulation des Equations Différentielles Stochastiques sous R de A. C. Guidoum.