Les réseaux de neurones

Warren McCulloch (à gauche) et Walter Pitts (à droite)

Historique :

Sommaire :

• Présentation
• Les réseaux de neurones
  • Vocabulaire
  • L’algorithme
  • Autres particularités
  • Les réseaux à base radiale
• Annexe théorique
• Exemple
• Application sous R
• Application sous SAS
• Bibliographie

Présentation :

Les réseaux de neurones ou neuronale, outil d’analyse supervisée qui prend ses racines dans les années 1940 et connait un essor constant de développement depuis, permet de discriminer une matrice de variables réponses de n’importe quel format (continue, binaire, etc.) à partir d’une matrice de variables explicatives, également de n’importe quel format, .

Les réseaux de neurones se sont construits une solide réputation au fil du temps, marquée par des hauts et des bas, dépendante de l’engouement mais aussi de la lassitude du moment. Relégués au statut de boîte noire, ils demeurent aussi riches que leur histoire. Initialement conceptualisés par Warren McCulloch et Walter Pitts en 1943, introduisant la notion de neurone formel, leur idée était de s’inspirer des neurones et des synapses du cerveau humain et de les mathématiser. Le concept a progressé, et en 1950, cette idée a pris forme avec la création du Perceptron par Frank Rosenblatt. Malheureusement, en 1969, Marvin Lee Minsky et Seymour Papert ont souligné d’importantes limites théoriques, entraînant une chute vertigineuse de l’enthousiasme généré, jusqu’au début des années 1980.

En 1982, John Joseph Hopfield introduit une version portant son propre nom et généralise la notion de base des neurones connectés de McCulloch et Pitts. Puis, en 1986, David Rumelhart, Geoffrey Hinton et Ronald J. Williams développent l’algorithme de rétropropagation du gradient pour l’apprentissage, faisant tomber un à un les détracteurs des réseaux de neurones. Cela ressuscite tout l’engouement qu’ils avaient généré autrefois et les propulse jusqu’à une utilisation courante en industrie à partir des années 1990. Leur essor reprend ainsi de plus belle et, dans les années 2000 avec l’augmentation exponentielle de la puissance de calcul des ordinateurs, valide l’arrivée des réseaux de neurones profonds (DNN), convolutionnels (CNN) et récurrents (RNN). Les désagréments théoriques balayés, les réseaux de neurones peuvent s’épanouir, permettant des avancées significatives dans le domaine du traitement du langage naturel. Depuis les années 2010, ils accumulent de nombreux succès remarquables dans divers domaines tels que le traitement de l’image, la traduction automatisée et la santé.

Malgré les éloges envers les réseaux de neurones, il faut rappeler qu’il s’agit d’un outil d’une haute complexité, manquant de lisibilité, capable de reproduire n’importe quelle fonction, notamment en raison de leur paramétrage et du risque accru de sur-apprentissage du phénomène que l’on cherche à modéliser ou encore de la convergence vers une solution globale et non locale. D’une certaine manière, ils sont déjà limités à une utilisation sur de grandes bases de données pour justement minimiser ce risque.

Enfin, bien que présentés ici comme un outil de classification et de prédiction, il existe également une version pour mener des analyses non supervisées, comme les cartes auto-organisatrices de Kohonen.

Les réseaux de neurones :

Hypothèse préliminaire : Tout format de variable et .

Vocabulaire

Avant de se lancer dans une vision plus approfondie des réseaux de neurones, il est important de rappeler le vocabulaire associé.

– Neurones, ou nœuds, et connexions synaptiques : unités de traitement, ou calculateur, interconnectées par des poids synaptiques. Chaque connexion synaptique a un poids qui détermine l’importance de la contribution d’un neurone à l’activation d’un autre ;

– Architecture ou topologie : structure du réseau distinguée généralement selon trois types. La couche d’entrée qui recevra les données initiales, les couches cachées qui effectueront les transformations intermédiaires, la couche de sortie qui retournera la modélisation finale. Dès lors où l’on aura plusieurs couches cachées on parlera de réseaux de neurones profonds ;

– Fonction d’activation ou de transfert : introduit la non-linéarité dans le réseau et ainsi la capacité de cet outil à modéliser des relations complexes. Cette dernière interviendra lors de la propagation avant alors que sa dérivée interviendra lors de la rétropropagation ;

– Propagation avant (feedforward) : les données circulent à travers le réseau de la couche d’entrée à la couche de sortie sans rétroaction. Chaque neurone transmet son activation aux neurones de la couche suivante. Il s’agit de la partie non supervisée de l’algorithme car ne faisant pas intervenir la réponse ;

– Rétropropagation (backpropagation) : ajustement des poids synaptiques du réseau en fonction de l’erreur calculée entre la sortie prédite et la sortie réelle. Son objectif est de minimiser cette erreur en temps réel, en ajustant les poids de manière itérative. il s’agit de la partie supervisée de l’algorithme ;

– Fonction de coût : mesure de l’écart entre la sortie prédite et la sortie réelle que la rétropropagation va chercher à chaque itération de minimiser ;

– Taux d’apprentissage : servant à déterminer la taille du pas que l’algorithme de rétropropagation prend pour ajuster les poids du réseau. Plus il est haut et plus la convergence est rapide au risque de s’arrêter sur une solution locale et non globale. Alors que plus il est faible, plus l’on devra utiliser d’itérations pour obtenir la convergence, favorisant ainsi les chances de trouver la solution globale.

Enfin, afin d’avoir une vision simple de toutes ces notions, on conclura avec la graphique suivant :

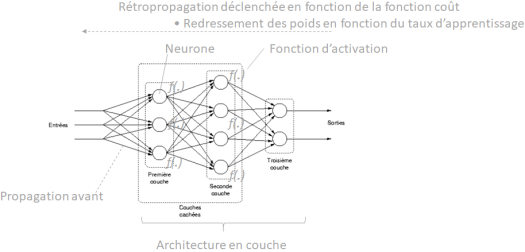
L’algorithme

On part d’une matrice , avec  variables explicatives et variables à prédire.

L’algorithme que l’on proposera n’intègre que les concepts de rétropropagation et d’apprentissage profond. Il s’approche plus particulièrement d’un type de réseau de neurones qui porte le nom de Perceptron multicouche. En voici les différentes étapes :

Etape 1 : Choix du paramétrage du réseau de neurones,

• On définit le nombre de couches cachées. Pour chaque couche , on désigne un nombre de neurones . On a volontairement mis la paramétrage possible à couche cachée afin de rappeler qu’il est possible, revenant à faire une simple régression linéaire ou logistique en fonction de la fonction d’activation choisie. Plus l’on ajoute de couches cachées et plus le pouvoir prédictif du modèle s’en voit amélioré, mais c’est aussi là que réside l’un des plus gros risques de surapprentissage. De nombreux auteurs proposent des méthodes différentes pour le choix du nombre de couches cachées. S. Tufféry, par exemple, indique qu’il faut compter à individus pour ajuster chaque poids et qu’il vaut mieux se concentrer sur l’utilisation au maximum de deux couches cachées puis jouer sur les autres paramètres pour améliorer son réseau de neurones. 
• On définit la fonction d’activation. La plus communément utilisée est la fonction logistique ou sigmoïde et de dérivée : . Mais on en retrouve d’autres qui le sont également dans une moindre mesure,

– ReLU (Rectified Linear Unit) : , appréciée par sa simplicité et sa capacité à résourdre le problème du gradient pour certaines types de réseau. Sa dérivée est si et si ;

– Leaky ReLU (Unité Linéaire Paramétrique) : , variation de ReLU permettant l’utilisation d’un « petit » gradient lorsque l’entrée est négative. Sa dérivée est si et si . On peut également parler de la version Parametric ReLU (PreLU) avec qui n’est plus fixé comme un paramètre mais va bénéficier du processus d’apprentissage de l’algorithme pour s’optimiser ;

– Tangente hyperbolique : , similaire à la fonction sigmoïde mais bornée sur , utile pour certains types de réseau nécessitant que les données soient normalisées. Sa dérivée est ;

– ELU (Unité Linéaire Exponentielle) : si , si , introduisant le concept de saturation pour les valeurs négatives du fait de la convergence vers de l’exponentielle dans ces cas-là. Sa dérivée est si , si ;

– Softmax : , à privilégier dans le cadre où est composée d’une ou plusieurs variable(s) multiclasse(s), il convient alors en amont d’en produire le tableau disjonctif complet. D’ailleurs, la remarque s’applique également si c’est le cas de . Sa dérivée est si et si ;

– Swish : , avec la fonction sigmoïde, permettant d’améliorer les performances dans certains cas de l’utilisation de la fonction ReLU. Sa dérivée est .

Le choix de la fonction d’activation se fait en lien avec la nécessité d’avoir une fonction linéaire au voisinage de et non linéaire aux extrémités. Enfin, la standardisation ou la normalisation des données est souvent conseillée en privilégiant des variables variant dans ou afin de contrôler le calcul des poids, favorisant alors certaines variables au détriment de la qualité prédictive du modèle final.

• On définit les poids (synaptiques) initiaux associés aux différentes couches. De préférence, aléatoirement. En effet, démarrer avec des poids identiques risque fortement d’entrainer la non-différenciation des neurones. Ce phénomène est connu sous le terme de « problème des neurones morts », diminuant leur capacité d’apprentissage. Xavier Glorot propose de délimiter le périmètre de tirage en divisant chacun des poids par : . Pour chacune des couches cachées , on notera la matrice des poids de taille si , si . Enfin, il faut également attribuer à la couche de sortie ses propres pondérations , tirées de la même manière et de taille . A noter que l’ajout de systématiquement est lié au besoin d’avoir, sans que cela soit obligatoire mais simplement conseillé, une ligne supplémentaire de poids associés aux termes constants.
• On définit le taux d’apprentissage , qui servira à fixer la vitesse de correction des matrices de pondérations. Ce dernier étant un pourcentage, il doit être compris dans ;
• On définit un nombre d’itérations à appliquer afin d’arrêter l’algorithme qu’il converge ou non.

Etape 2 : Propagation avant (apprentissage non supervisé), en notant le produit matricielle, on applique l’algorithme suivant,

• Pour la première couche cachée : ;
• Dès la seconde couche cachée : ;
• Pour la couche de sortie :

En fait, cette étape de l’algorithme remet un peu en question la vision traditionnelle du réseau de neurones que l’on veut à tout prix opposer à celle du cerveau, ce qui est normal puisqu’il s’agit du concept de base à l’origine de l’outil. Mais on comprend mieux certaines présentations qui consistent à le représenter comme une succession de « plaques » contre lesquels l’on va jeter notre jeu de données, l’éparpillant matriciellement pour à nouveau le rejeter comme une nouvelle plaque qui va l’éparpiller à son tour. Et ainsi de suite jusqu’à ce qu’à force d’exploser nos données, elles finissent par se remettre dans le bon ordre. On retrouve ici l’approche non supervisée puisque l’on n’utilise pas notre réponse dans la propagation.

Enfin, à noter que cette partie de l’algorithme fait également aussi office de règle décisionnelle. Munis des poids et d’un nouvel individu décrit selon les caractéristiques utilisées pour le paramétrage, il suffit d’appliquer les itérations indiquées précédemment pour obtenir sa prédiction.

Etape 3 : Calcul de l’erreur, on compare la sortie prédite avec la réponse en utilisant une fonction de coût. Cette fonction mesure la différence entre la prédiction du réseau et les classes réelles. On a l’embarras du choix à nouveau :

– L’erreur quadratique moyenne (MSE) : , le classique du genre. On peut précéder à sa variante consistant à appliquer le facteur au lieu de ou encore celle s’affranchissant de l’élévation au carré pour les valeurs absolues (MAE), moins sensible aux valeurs aberrantes que la MSE. Elles sont alors réservée à une ou plusieurs réponse(s) continue(s) ;

– L’entropie croisée binaire (Binary Cross-Entropy) : , réservée à une réponse univariée binaire et donc souvent associée à la fonction d’activation sigmoïde ;

– L’entropie croisée catégorielle (Categorical Cross-Entropy) : , réservée à une réponse univariée à plusieurs classes et donc souvent associée à la fonction d’activation softmax.

Etape 4 : Rétropropagation (apprentissage supervisé), l’erreur calculée est propagée en sens inverse à travers le réseau. Les poids synaptiques sont ajustés de manière itérative pour minimiser cette erreur. Cela se fait en utilisant la descente de gradient, où la dérivée partielle de la fonction de coût. en notant le produit terme à terme,

– On démarre sur la couche de sortie,

• Initialiser , sachant que certains réseaux programmés font intervenir la dérivée de la fonction coût à la place de la formule proposée ;
• Calculer les corrections des poids de la couche de sortie

– Puis sur la dernière couche cachée,

• Mettre à jour la dérivation , la matrice des poids de la couche de sortie est utilisée cette fois-ci en lui retirant la première ligne ;
• Calculer les corrections des poids de la dernière couche cachée en faisant intervenir la dérivée de la fonction d’activation , et en notant le produit terme à terme, 

– Puis en poursuivant couche par couche en sens inverse, ,

• Itérativement mettre à jour la dérivation , la matrice des poids de la couche est utilisée en lui ôtant la première ligne ;
• Calculer les corrections des poids de la couche ,

– Enfin, une fois arrivé à la première couche,

• On met à jour la dérivation , la matrice des poids de la seconde couche est utilisée en lui supprimant la première ligne ;
• Calculer les corrections des poids de la première couche,

Etape 5 : On dispose désormais des matrices de correction des différentes couches . Et on applique ces corrections en une seule fois : 

L’algorithme de la descente du gradient, présenté ici, est le plus répandu mais demeure cependant sensible aux minimums locaux. Parmi les autres méthodes existantes : l’algorithme de Levenberg-Marquardt optimal pour les petits réseaux, quasi-Newton, gradient conjugué meilleur compromis pour les réseaux complexes, propagation rapide ou encore les algorithmes génétiques. Concernant celui présenté ici, on peut retrouver dans la littérature plusieurs amélioration comme l’optimisation stochastique, la régularisation (pour éviter le surapprentissage) et des techniques avancées telles que les algorithmes Adam, RMSprop, etc.

– Etape 6 : Sur le nombre d’itérations défini en guise de paramétrage, on répète les étapes à jusqu’à ce que le modèle atteigne une performance satisfaisante sur les données d’entraînement.

Enfin, et comme tout bon outil de type data mining, il convient de valider le modèle construit par précédés empiriques. On lance alors ces étapes sur un échantillon d’apprentissage obtenu soit en scindant l’échantillon de base (cross-validation, LOOCV, tirage aléatoire de deux tiers de l’échantillon) et de valider la modèle « tuné » obtenu sur un échantillon test. L’objectif étant d’obtenir les mêmes performances sur échantillon test et échantillon de validation. Si c’est le cas on peut le valider, sinon il faut en reconstruire un nouveau.

Autres particularités

Comme indiqué, l’algorithme présenté ici est assez incomplet vis à vis de ceux des véritables réseaux de neurones implémentés sur bon nombre de langage de programmation de nos jours. Parmi les nombreux concepts non évoqués précédemment on a :

– La convolution, donnant leur nom aux réseaux CNN, consiste à appliquer un filtre (ou noyau) directement sur . Son but est de détecter les motifs spatiaux dans les données d’entrée. Si l’on avait voulu intégrer ce concept dans l’algorithme présenté ci-dessus, grosso-modo il aurait fallu définir de deux nouveaux jeux de pondérations dédiés (filtres), appliquer la convolution des données d’origine avec le premier filtre translaté par le second. Cela définit l’étape en amont, ensuite on applique les étapes suivantes pour la propagation. Pour la rétropropagation, l’application de la convolution se fait cette fois-ci à la toute fin de l’algorithme, via processus inversé.

– La normalisation par lots (Batch Normalization) est un concept introduit pour résoudre les problèmes de convergence « lente », d’explosions du gradients et ainsi gagner en stabilité du modèle. Initialement développé pour les CNN, elle est désormais utilisée pour tout type de réseau. Il s’agit de composer un certain nombres de sous-échantillon des données d’origine, appelés mini-batch, et pour chaque sortie de neurone , on va appliquer la Batch Normalisation au travers de la formule suivante :

, avec paramètre d’échelle, paramètre de translation et constante ajoutée pour évitée la division par . A noter qu’il y a autant de paramétrages que de couches cachées considérées dans la structure du réseau.

Concrètement et si l’on reprenait l’algorithme décrit, cela reviendrait à appliquer la fonction d’activation après Batch Normalisation du produit scalaire pour la propagation. Et lors de la rétropropagation, appliquer le processus de calcul inversé sur et à chaque couche. Une fois de plus, le paramètre , taux d’apprentissage, servira à fixer à quelle vitesse on rectifie les paramètres et .

Un mot sur le réseau résiduel (Residual Networks ou ResNets) dont le concept vise à introduire des sauts de connexion pour faciliter le flux d’information à travers le réseau, permettant l’entrainement de réseaux beaucoup plus profonds. Souvent couplé à la Batch Normalisation, il s’agit alors de l’appliquer sur certaines couches et pas systématiquement à toutes.

– Et encore de nombreux et autres nombreux concepts, tels que les fonctions d’erreur ou coût adaptatives, les méthodes de régularisation (régression Ridge, Lasso, Elasticnet, etc.), les méthodes des moments permettant de contrôler le risque que les pondérations partent dans un unique sens et aillent s’enterrer vers une solution locale, etc., que l’on ne définira pas ici. L’on invitera alors le lecteur à se fournir en ouvrage spécialisé sur le sujet tant il y en a pléthore.

Les réseaux à base radiale :

On dénombre énormément de type de réseaux différents, adaptés selon le format des données en entrée comme par exemple celles appariées ou temporelles. Une fois de plus, il est conseillé de s’orienter ensuite vers des ouvrages spécialisés. Toutefois, on pourra laisser un mot sur l’une des alternatives les plus connues au Perceptron Multicouche, les réseaux à base radiale (RBF).

Ils se distinguent par une architecture composée d’une couche d’entrée, d’une unique couche cachée utilisant des fonctions radiales comme la fonction gaussienne avec distance euclidienne entre le point d’entrée et le centre et le paramètre de largeur gaussienne ou écart-type, et d’une couche de sortie. La notion de centre dans un RBF consiste à en définir un pour chaque neurone de la couche cachée, soit un point dans l’espace d’entrée du réseau. 

Les RBF présentent les avantages d’une capacité à apprendre à modéliser des relations non linéaires grâce aux fonctions radiales et sont moins sensibles au surajustement par rapport au Perceptron Multicouche. Quant aux inconvénients majeurs, ils nécessitent la sélection des centres et des paramètres radiaux parfois difficile ainsi que des performances potentiellement inférieures sur des tâches plus complexes comparées aux Perceptron Multicouche.

Annexe théorique :

On présentera ici une esquisse de la démonstration de l’apport de l’algorithme de rétropropagation sur la qualité de modélisation des réseaux de neurones.
En notant le taux d’apprentissage, poids de la couche cachée , l’algorithme de la descente de gradient lors de l’étape de rétropropagation s’exprime ainsi :

L’apport de la rétropropagation sur l’estimation des paramètres provient du terme qui est l’erreur de prédiction et servira à ajuster et réajuster les matrices des poids de chaque couche. En notant la fonction coût qui mesure l’écart entre valeurs prédites et valeurs réelles, On peut plus précisément écrire :

, avec,

– mesure comment le coût varie par rapport à la sortie de la couche de sortie. Cela donne une indication de la sensibilité de la fonction de coût aux changements dans la prédiction ;

– représente la dérivée de la fonction d’activation par rapport à son entrée. Cette dérivée mesure comment de petits changements dans l’entrée de la couche de sortie affectent la sortie elle-même.

Maintenant, pour le taux d’apprentissage , on applique la fonction coût à la formule d’actualisation des poids, et selon le développement de Taylor on a :

Si est faible, alors la mise à jour des poids est stable, tandis que si elle est importante, la mise à jour devient significative. Dès lors, le taux d’apprentissage va permettre un équilinre entre converge rapide et stabilité à l’entraînement.

Exemple :

Soit l’échantillon suivant,

Ci-dessous le nuage de point basé sur ces données,

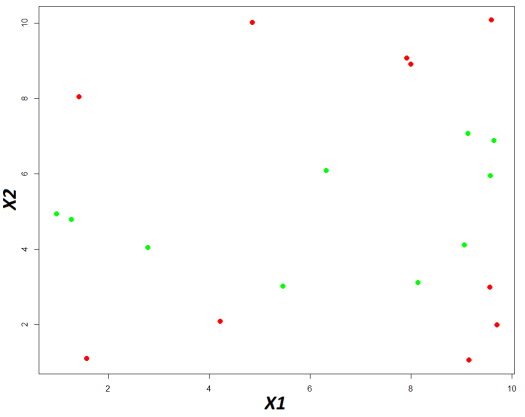
En vert la classe « A » et en rouge la classe « B »

On cherche donc à déterminer une fonction permettant de prédire les deux classes de en fonction des valeurs de . Comme il s’agit d’un exemple, on s’affranchira de la construction par apprentissage statistique. De plus, on ne procèdera pas à la standardisation des variables en amont.

On opte pour le paramétrage suivant :

– Une architecture formée d’une couche d’entrée à neurones (en lien avec le nombre de variables explicatives). couches cachées, l’une à neurones et la seconde à neurones, et une couche de sortie à un neurone (en lien avec le nombre de variable à prédire et son nombre de classes) ;

– La fonction d’activation choisie sera la fonction sigmoïde : , de dérivée ;

– La fonction coût : ;

– Le taux d’apprentissage : ;

– Et pour les poids, on tire aléatoirement ceux associés à la première couche cachée de taille , nombre de neurones de la couche d’entrée, soit deux car deux variables explicatives et nombre de neurones paramétrée sur cette couche cachée :

, à la seconde couche cachée de taille (nombre de neurones de la première couche cachée puis de la seconde couche) :

, et à la couche de sortie de taille (nombre de neurones de la seconde et dernière couche et nombre de réponse de , ici une seule) : 

L’étape d’initialisation étant réglée, on passe à la suite avec l’utilisation de l’algorithme de propagation avant. Donc, pour l’itération N° ,

– La phase de propagation, en débutant par celle dans la première couche se calcul via :

On obtient alors,

– Pour celle de la seconde couche :

– Et enfin, la couche de sortie :

Avant de passer à l’étape de rétropropagation, on calcul le taux d’erreur global, en créant un vecteur numérique associé à la réponse , le fixant à pour la classe « A » et à pour la classe « B ». Selon la fonction coût retenue :

– La phase de rétropropagation. Avant, on va calculer et incrémenter le terme : 

, et maintenant la matrice correctrice des poids associées à la couche de sortie :

Avant de procéder à la rétropropagation sur la seconde couche cachée, on met à jour :

Et puis on travaille sur la seconde couche, en faisant intervenir la dérivée de la fonction d’activation, d’où l’utilisation du terme :

Avant de boucler la rétropropagation, on met à nouveau à jour :

Et enfin, on travaille sur la première couche cachée, en faisant à nouveau intervenir la dérivée de la fonction d’activation :

Les termes d’ajustement sont désormais tous déterminés, il ne reste plus qu’à les appliquer :

–

–

–

Les trois jeux de pondérations étant désormais mis à jour, on peut lancer la seconde itération. Sans reprendre les calculs, car il s’agit exactement des mêmes et seul vont changer, on obtiendra pour itérations, la courbe de l’évolution de l’erreur de prédiction suivante :

Au bout de itérations, l’algorithme converge. On a ainsi les pondérations finales suivantes :

Les performances obtenues peuvent être décrites au travers de la matrice de confusion suivante :

, soit un taux de bonne classification globale de . Enfin, et plus concrètement, on peut afficher le découpage du plan comparé aux classes réelles.

Les bandes rouges correspondent à la région de la classe « A » construite par le modèle, en bleu celle de la classe « B ». En rouge les données réelles de la classe « A » et en vert celles de la classe « B »

Application sous R :

Soit l’exemple suivant :

BDD = data.frame(Y = c(rep(0,10),rep(1,10)),
X1 = c(8.1472, 9.0579, 1.2699, 9.1338, 6.3236, 0.9754, 2.7850, 5.4688, 9.5751, 9.6489, 1.5761, 9.7059, 9.5717, 4.8538, 8.0028, 1.4189, 4.2176, 9.1574, 7.9221, 9.5949),
X2 = c(3.1101, 4.1008, 4.7876, 7.0677, 6.0858, 4.9309, 4.0449, 3.0101, 5.9496, 6.8729, 1.0898, 1.9868, 2.9853, 10.0080, 8.9052, 8.0411, 2.0826, 1.0536, 9.0649, 10.0826))

Package et fonction R: neuralnet: Training of Neural Networks (r-project.org)

La fonction neuralnet du package du même nom permet de réaliser des réseaux de neurones. Après chargement du package, on lance sa conception de la manière suivante :

neuralnet(Y ~ x1 + x2, data = BDD, hidden = c(3,6), algorithm = « backprop », learningrate = 0.1, act.fct = « logistic », linear.output = FALSE, lifesign = « full », constant = TRUE)

Parmi les éléments à insérer les plus importants il faut relever :

–  La formule définissant variable réponse (à gauche) et variables explicatives (à droite) : ~ ;

–  La base de données sur laquelle on souhaite travailler : ;

– Le nombre de couches cachées et de neurones par couche : ;

– L’utilisation de l’algorithme de rétropropagation : ;

– Le taux d’apprentissage nécessaire pour définir la vitesse à laquelle on rectifie les pondérations : ;

– La fonction d’activation, ici la fonction sigmoïde : ;

– L’affichage de tous les résultats obtenus : ; 

– Le choix d’un modèle non linéraire : .

On obtient alors les résultats suivants :

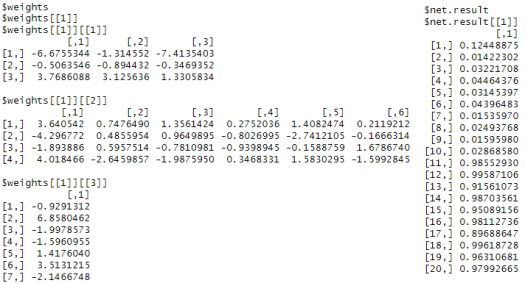
, avec, à gauche, les poids finaux par couche et, à droite, les scores de prédiction.

Les différences obtenues avec les calculs manuels (cf partie « Exemple ») sont explicables du fait que la fonction neuralnet est bien plus complète et permet de lancer des réseaux de neurones bien plus élaborés que celui présenté dans cet article.

Application sous SAS :

Soit l’exemple suivant :

data BDD;
input x1 x2 Y;
cards;
8.1472 3.1101 0
9.0579 4.1008 0
1.2699 4.7876 0
9.1338 7.0677 0
6.3236 6.0858 0
0.9754 4.9309 0
2.7850 4.0449 0
5.4688 3.0101 0
9.5751 5.9495 0
9.6489 6.8729 0
1.5761 1.0898 1
9.7059 1.9868 1
9.5717 2.9853 1
4.8538 10.0080 1
8.0028 8.9052 1
1.4189 8.0411 1
4.2176 2.0826 1
9.1574 1.0536 1
7.9221 9.0649 1
9.5949 10.0826 1
;
run;

Le logiciel SAS offre un module complet pour la production de réseaux de neurones : SAS Visual Data Mining and Machine Learning. Cependant, ce dernier n’est pas disponible dans le package de base, tout comme le module IML pour les calculs matriciels. Par conséquent, on proposera la macro suivante :

%macro neuralNetwork(DATA =, REPONSE =, W =, LEARN_RATE =, ITERATION =, TYPE =);

/* La macro neuralNetwork est disponible pour concevoir son propre réseau de neurones. Sur cette première version, il n’est pas possible de traiter plusieurs réponses Y à la fois. Concernant l’architecture, elle se déploie automatiquement en fonction des matrices de pondérations insérées dans le paramétrage. Par défaut, le programme n’a été implémenté que pour la fonction sigmoïde, des indications dans le code permettent de voir où porter les modifications pour l’ajout d’autres fonctions d’activation.

Paramètres : La base de données DATA et le nom de la variable à discriminer REPONSE, la liste des matrices/vecteurs de pondération W, le taux d’apprentissage LEARN_RATE, le nombre d’itérations à exécuter ITERATION. Si l’on veut utiliser la macro pour classer un nouvelle individu TYPE = C ou pour tuner ses paramètres TYPE = M.

Le programme n’ayant été testé que pour l’exemple qui suit, il est important de conserver les mêmes noms de variables et structure des données. Des mises à jour seront réalisées dans le temps, ajoutant d’autres fonctionnalités */

/* Paramétrage des fonctions pour n’afficher que les erreurs et les warnings */ 

options nonotes spool;

/* Si on veut classer un nouvelle individu, alors on se débarrasse du paramètre sur les itérations en le fixant à 1 puisqu’il s’agit d’utiliser uniquement que la propagation sur les paramètres entrés */

%if &TYPE. = C %then %do;

%let ITERATION = 1;

%put Classification;

%let Obj = Classification;

%end;

/* On renvoi les paramètres du réseau en fonction des matrices des poids utilisées */

%let nbc = %eval(%sysfunc(countw(&W.)));

%do couche = 1 %to &nbc.;

%if &couche. < &nbc. %then %do;

proc contents data = W&couche. out = biblio noprint;

run;

proc sql noprint;

select count(*) into: nb_neurones from biblio;

quit;

%if &couche. = 1 %then %do;

%let neurones = &nb_neurones.;

%end;

%if &couche. > 1 %then %do;

%let neurones = &neurones. &nb_neurones.;

%end;

%end;

%end;

%put Au regard du paramétrage, le réseau programmé aura &nbc. couches cachées, de nombre de neurones respectifs : &neurones.;

/* Pour chaque itération, on applique les étapes de propagation et rétropropagation */

%do it = 1 %to &ITERATION.;

%if &TYPE. = M %then %do;

%put Modélisation;

%put Itération N° &it. sur &ITERATION.;

%let Obj = Modélisation;

%end;

%put Application de la propagation dans un objectif de &Obj.;

/* On lance la propagation pour chaque couche indirectement paramétrée via les poids insérés */

%do couche = 1 %to &nbc.;

%put Sur couche &couche.;

%let cmu = %eval(&couche. – 1);

/* Constitution de la matrice de gauche pour le produit scalaire (1,X) %*% W */

data I_data;

/* Si première couche alors X est la matrice de données d’origine */

%if &couche. = 1 %then %do;

set &DATA.;

drop &REPONSE.;

%end;

/* Pour les couches suivantes, X est H de la couche moins un */

%if &couche. > 1 %then %do;

set H&cmu.;

%end;

/* On créé le colonne associée à la constante de régression */

Cst = 1;

run;

/* L’ordre étant primordial pour le bon déroulement de l’algorithme, on s’assure que la colonne Cst est bien en première */

proc contents data = I_data out = biblio noprint;

run;

proc sql noprint;

select(name) into: list_var separated by ‘,’ from biblio where name ne « Cst »;

quit;

proc sql noprint;

create table I_dataf as select Cst, &list_var. from I_data;

quit;

/* Application du produit sclaire (1,X) %*% W en prenant les bons X et W en lien avec la couche en cours, on créé alors nos matrices H */

%produit_scalaire(A = I_dataf, B = W&couche., Activation = 1);

data H&couche.;

set ResultF;

run;

%end;

/* Si on cherche juste à classifier, alors l’algorithme s’arrête, dans le cas où l’on veut tuner nos paramètres/modéliser, on applique la rétropropagation */

%if &TYPE. = M %then %do;

/* On calcul l’erreur de prédiction afin de constituer le vecteur que l’on pourrait ploter pour voir sa convergence, mais également l’erreur par simple différence nécessaire aux calculs à venir */

data Erreur;

merge &DATA. H&nbc.;

/* Choix de la fonction erreur et sa dérivée */

Erreur = (col1 – &REPONSE.);

Erreur2 = Erreur**2;

keep Erreur Erreur2;

run;

proc sql noprint;

select sum(Erreur2) into: Erreur from Erreur;

quit;

/* Ajout de la nouvelle Erreur calculée aux autres */

data Courbe_erreur_add;

Erreur = 0.5*&Erreur.;

run;

%if &it. = 1 %then %do;

data Courbe_erreur;

set Courbe_erreur_add;

run;

%end;

%if &it. > 1 %then %do;

data Courbe_erreur;

set Courbe_erreur Courbe_erreur_add;

run;

%end;

%put Application de la rétropropagation pour la Modélisation;

/* Algorithme de rétropropagation */

%do couche = 1 %to &nbc.;

/* On inverse l’incrémentation pour retrouver la logique backward */

%let couche_retro = %eval(-(&couche. – &nbc. – 1));

%let cmu = %eval(&couche_retro. – 1);

%put Sur couche &couche_retro.;

/* On crée la matrice t(1,H), matrice à gauche du produit scalaire */

data I_data;

/* En bout de rétropropagation, H est les données d’origine */

%if &couche_retro. = 1 %then %do;

set &DATA.;

drop &REPONSE.;

%end;

/* Sur les couches en sens inverse, on prend le H calculé lors de la propagation */

%if &couche_retro. > 1 %then %do;

set H&cmu.;

%end;

/* On rajoute la Constante */

Cst = 1;

run;

/* On s’assure que la Constante est bien en première colonne */

proc contents data = I_data out = biblio noprint;

run;

proc sql noprint;

select(name) into: list_var separated by ‘,’ from biblio where name ne « Cst »;

quit;

proc sql noprint;

create table I_dataf as select Cst, &list_var. from I_data;

quit;

proc transpose data = I_dataf out = T_I_dataG;

run;

data T_I_dataG;

set T_I_dataG;

drop _name_;

run;

/* Sur la première couche rétropropagée, à savoir la dernière du réseau, on applique la formule t(1,H) %*% fonction coût ou sa dérivée */

%if &couche_retro. = &nbc. %then %do;

/* Matrice à droite du produit scalaire */

data H;

set Erreur;

keep Erreur;

run;

/* Application du produit scalaire et création de la matrice correctice des poids de la dernière couche */

%produit_scalaire(A = T_I_dataG, B = H, Activation = 0);

data dW&couche_retro.;

set ResultF;

run;

%end;

%let nbc_mu = %eval(&nbc. – 1);

%let nbc_md = %eval(&nbc. – 2);

%if &couche_retro. < &nbc. %then %do;

/* Pour les couches, en sens inverse, suivantes, on créé la matrice à droite */

proc contents data = H&couche_retro. out = biblio noprint;

run;

proc sql noprint;

select(name) into: list_mu separated by ‘ ‘ from biblio;

select count(*) into: nb_mu from biblio;

quit;

data H;

merge H&couche_retro.;

%do vmu = 1 %to &nb_mu.;

/* Application de la dérivée de la fonction d’activation, ici la fonction sigmoïde. Afin d’étendre le programme à d’autres fonctions d’activation, il convient de réaliser les ajouts ici de leur dérivée */

h_%scan(&list_mu.,&vmu.,’ ‘) = %scan(&list_mu.,&vmu.,’ ‘) * (1 – %scan(&list_mu.,&vmu.,’ ‘));

drop %scan(&list_mu.,&vmu.,’ ‘);

%end;

run;

/* On récupére la bonne matrice des poids associés à la couche en cours de traitement */

%let cr_pu = %eval(&couche_retro. + 1);

data T_W;

set W&cr_pu.;

/* A laquelle on supprime la première ligne, que l’on transpose ensuite */

if _n_ ne 1;

run;

proc transpose data = T_W out = T_W;

run;

data T_W;

set T_W;

drop _NAME_;

run;

/* Si on est à l’avant-dernière couche, alors exceptionnellement, on prend l’erreur ou sa dérivée directement */

%if &couche_retro. = &nbc_mu. %then %do;

data Erreur;

set Erreur;

drop Erreur2;

run;

%produit_scalaire(A = Erreur, B = T_W, Activation = 0);

/* Et comme pour les couches qui vont suivre on incrémente la dérivation, on l’enregistre afin de l’ajustement couche par couche */

data dh;

set ResultF;

run;

%end;

/* A partir de l’avant-avant-dernière couche, on peut plus facilement automatiser en prenant la dérivation dh incrémentée et l’appliquer directement */

%if &couche_retro. <= &nbc_md. %then %do;

%produit_scalaire(A = dh, B = T_W, Activation = 0);

data dh;

set ResultF;

run;

%end;

/* Reste un dernier produit scalaire à exécuter et sur les matrices réassemblées à gauche et à droite */

data T_I_dataD;

merge H dh;

%do vmu = 1 %to &nb_mu.;

hh_%scan(&list_mu.,&vmu.,’ ‘) = h_%scan(&list_mu.,&vmu.,’ ‘) * %scan(&list_mu.,&vmu.,’ ‘);

drop h_%scan(&list_mu.,&vmu.,’ ‘) %scan(&list_mu.,&vmu.,’ ‘);

%end;

run;

%produit_scalaire(A = T_I_dataG, B = T_I_dataD, Activation = 0);

/* On obtient alors les autres matrices correctices des poids */

data dW&couche_retro.;

set ResultF;

run;

%end;

%end;

/* On applique les corrections dW à nos poids W et ensuite on peut passer à l’itération suivante avec les nouveaux W mis à jour */

%put Mise à jour des poids;

%do couche = 1 %to &nbc.;

proc contents data = W&couche. out = biblio noprint;

run;

proc sql noprint;

select (name) into: list_w separated by ‘ ‘ from biblio;

select count(*) into: nb_w from biblio;

quit;

proc contents data = dW&couche. out = biblio noprint;

run;

proc sql noprint;

select (name) into: list_dw separated by ‘ ‘ from biblio;

quit;

data W&couche.;

merge W&couche. dW&couche.;

%do w = 1 %to &nb_w.;

%scan(&list_w.,&w.,’ ‘) = %scan(&list_w.,&w.,’ ‘) – &LEARN_RATE.*%scan(&list_dw.,&w.,’ ‘);

drop %scan(&list_dw.,&w.,’ ‘);

%end;

run;

%end;

%end;

%end;

/* Que ce soit pour du tuning/modélisation de paramètres, ou de la classification directement, on renvoie la matrice d’origine avec le résultats de ces prévisions que l’on peut traiter à part */

data Classification;

merge &DATA. H&nbc.;

run;

/* Suppression des différentes tables annexes utilisées et sans intérêt */

proc datasets lib = work nolist;

delete varA varB PA PB prod_scal result_add resultF result I_data biblio I_dataF erreur T_I_dataG T_I_dataD dH H T_w courbe_erreur_add;

%do d = 1 %to &nbc.;

delete H&d. Dw&d.;

%end;

run;

/* Réinitialisation des paramètres de la log */

options notes nospool;

%mend;

, qu’il faudra coupler à la macro suivante permettant de calculer les produits scalaires nécessaires :

%macro produit_scalaire(A=, B=, Activation=);

/* Macro pour réaliser un produit scalaire entre deux matrices/vecteurs de données 

   Paramètres : la matrice de gauche A, la matrice de droite B, et si oui (1) ou non (0) on applique au résultat du produit scalaire la fonction d’activation pour chaque cellule/terme. Sur cette première version, seule la fonction sigmoïde a été codée */

/* Nombre de lignes de la matrice de gauche */ 

proc sql noprint;

select count(*) into: nbA from &A.;

quit;

/* Nombre de colonnes de la matrice de droite */

proc contents data = &B. out = varB noprint;

run;

proc sql noprint;

select count(*) into: varB from varB;

select (name) into: listB separated by ‘ ‘ from varB;

quit;

/* Application du produit scolaire */

%do l = 1 %to &nbA.;

%do c = 1 %to &varB.;

/* On récupère les éléments de la ligne l de la matrice de gauche */

data PA;

set &A.;

if _n_ = &l.;

run;

proc transpose data = PA out = PA;

run;

/* On récupère les éléments de la colonne c de la matrice de droite */

data PB;

set &B.;

rename %scan(&listB.,&c.,’ ‘) = T_%scan(&listB.,&c.,’ ‘);

keep %scan(&listB.,&c.,’ ‘);

run;

/* On les superpose, afin de directement multiplier les deux vecteurs en cours de traitement */

data prod_scal;

merge PA PB;

prod = col1*T_%scan(&listB.,&c.,’ ‘);

run;

/* On somme les produits réalisés un à un */

proc sql noprint;

select sum(prod) into: prod_scal from prod_scal;

quit;

/* Adaptée au réseau de neurone, on propose ici de mettre directement l’application de la fonction d’activation ou non, on peut modifier le paramètre Activation si l’on souhaite rajouter d’autres fonctions */

data Result_add;

%if &Activation. = 1 %then %do;

/* Application de la fonction d’activation */

col&c. = 1/(1 + exp(-&prod_scal.));

%end;

%if &Activation. = 0 %then %do;

col&c. = &prod_scal.;

%end;

run;

/* On reconstitue la première ligne des résultats des différents produits scalaires */

%if &c. = 1 %then %do;

data Result;

set Result_add;

run;

%end;

%if &c. > 1 %then %do;

data Result;

merge Result Result_add;

run;

%end;

%end;

/* On rajoute ensuite les nouvelles lignes des résultats des différents produits scalaires */

%if &l. = 1 %then %do;

data ResultF;

set Result;

run;

%end;

%if &l. > 1 %then %do;

data ResultF;

set ResultF Result;

run;

%end;

%end;

%mend;

On lance le réseau de neurones dans un objectif de déterminer le modèle prédictif. On doit alors produire dans un premier temps les différents poids . Etant donné que l’on veut couches cachées à, respectivement, et neurones,

data w1;
input w1_1 w1_2 w1_3;
cards;
-0.5166363 0.9554752 -0.6368997
0.1703469 -0.8107111 -1.0079267
0.3509102 0.6576622 0.6678786
;
run;

data w2;
input w2_1 w2_2 w2_3 w2_4 w2_5 w2_6;
cards;
1.076244 1.2653173 1.6323954 0.26325727 0.1376167 1.0766192
-1.586651 0.3370436 0.5188823 0.65283448 -0.9157413 -0.6095473
-1.382789 0.7540253 -0.8235877 0.01111528 0.3684991 1.4985495
0.712537 -1.8088945 -1.2941944 -0.44789165 -0.1230735 -0.3934913
;
run;

data w3;
input w;
cards;
-0.1755870
1.2174536
0.8050443
0.4084043
1.3316199
1.2032622
-0.3737364
;
run;

On applique la macro de la manière suivante :

%neuralNetwork(DATA = BDD, REPONSE = Y, W = W1 W2 W3, LEARN_RATE = 0.1, ITERATION = 50, TYPE = M);

Parmi les éléments à insérer, il faut relever :

– Le tableau sur lequel on veut travailler : ;

– Le nom de la réponse à discriminer : ;

– La liste des matrices des poids : ;

– Le taux d’apprentissage, qui servira à définir à quel vitesse l’on applique les matrices correctrices des poids : ;

– Le nombre d’itérations à réaliser : ;

– Le mode d’utilisation de la macro : pour tuner les paramètres, pour classer un nouvel individu.

On obtient alors les résultats suivants parmi les tableaux générés en fin de procédure :

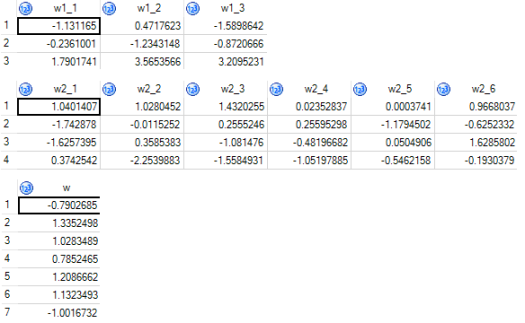
, puis :

, et :

La première série de tableaux présente les pondérations finales : . Le quatrième tableau, le taux d’erreur à chaque itération et le dernier la base de données d’origine à laquelle on a inséré les prédictions finales.

L’algorithme implémenté tel quel est particulièrement long en calcul, aussi il n’a été testé que pour itérations, réalisées en minutes, très fortement dépendant de la taille de la base de données du fait de l’application du produit scalaire.

Bibliographie :

– Probabilité, analyse des données et statistiques de Gilbert Saporta ;

– The Elements of Statsticial Learning de Trevor Hastie, Robert Tibshirani et Jerome Friedman ;

– Data mining et statistique décisionnelle, l’intelligence des données de Stéphane Tufféry ;

– Comprendre le deep learning, une introduction aux réseaux de neurones de Jean-Claude Heudin ;

– Le site web : https://datafuture.fr/post/fabrique-ton-premier-reseau-de-neurones/