Le test binomial

add

$\bullet$ Historique :

$\begin{tabular}{|l|c|c|} \hline Bloc & 13/09/2015-V1 & 25/02/2024-V2 \\ \hline Historique & & Cr\'eation \\ \hline Sommaire & & Cr\'eation \\ \hline Pr\'esentation & Cr\'eation & MAJ \\ \hline Le test & Cr\'eation & Ajout calcul p-valeur loi normale \\ \hline Tendance lorsque... & Cr\'eation & \\ \hline Annexe th\'eo... & Cr\'eation & MAJ \\ \hline Exemple & Cr\'eation & MAJ \\ \hline Appli... info... & Cr\'eation & Devient Appli... sous R \\ \hline Appli... sous SAS & & Cr\'eation \\ \hline Bibliographie & Cr\'eation & \\ \hline \end{tabular}$

$\bullet$ Sommaire :

Présentation
Le test
- La table de la loi centrée-réduite
- Calcul de la p-valeur exacte si $n < 25$
- Calcul de la p-valeur exacte si $n \geq 25$
- Tendance pour le rejet de $H_0$
Tendance lorsque $n \rightarrow + \infty$
Annexe théorique
Exemple
Application sous R
Application sous SAS
Bibliographie

$\bullet$ Présentation :

Le test binomial, également appelé test exact binomial, a été publié par Ronald Aylmer Fisher en 1925. Il s’agit d’une approche non paramétrique permettant de tester si la répartition des deux groupes d’une variable binaire $X$ est aléatoire.

A l’instar du test exact de Fisher, le test binomial est connu comme une alternative au test du $\chi ^2$ de Pearson lorsque la configuration des effectifs ne permet pas son application. Toutefois, lorsque $X$ a plus de deux modalités, c’est bien vers ce dernier (portant également le nom de test multinomial) qu’il convient de se tourner.

$\bullet$ Le test :

Hypothèse préliminaire : $X$ binaire.

La statistique de test binomial est,

$b = \mathbb{P}_{n,p} (n_1)$

Où $n_1$ est l’effectif du groupe d’intérêt de $X$ et fixé en amont par l’utilisateur, $p$ la probabilité de référence à laquelle on souhaite comparer les proportions observée et $\mathbb{P}_{.} (.)$ la probabilité associée à la loi Binomiale de paramètres $B(n,p)$ et de formule,

$\mathbb{P}_{n,p} (n_1) = \binom{n}{n_1} p ^{n_1} \cdot (1 - p) ^{n - n_1}$

Deux cas de figure sont à prendre en compte pour le calcul de la p-valeur associée à $b$ . Si $n < 25$ alors elle se détermine au travers de l’algorithme de Monte-Carlo et si $n \geq 25$ alors on calcule le z-score,

$z = |\frac{b - \mathbb{E}[b]}{\sigma_b}|$

, où $\mathbb{E}[b] = n \cdot p$ et $\sigma_b = \sqrt{n \cdot p \cdot (1 - p)}$ . Le z-score suit une loi normale centrée-réduite.

Que l’on fasse usage de la statistique de test $b$ ou $z$ , l’hypothèse $H_0$ reste :

Il n’y a pas de différence entre les fréquences observées et attendues / $\pi = p$

En restant sur le cas le plus fréquent et en lien avec des échantillons en général de grande taille, on pose $z_{\alpha, 0, 1}$ la valeur seuil de la distribution de la statistique de test $z$ pour une confiance $\alpha$ , et associée à une loi normale centrée-réduite, les hypothèses alternatives sont alors,

– $H_1: z > 0$ , soit $z > z_{1 - \alpha, 0, 1}$ , pour un test unilatéral à droite ;

– $H_1: z < 0$ , soit $z > z_{\alpha, 0, 1}$ , pour un test unilatéral à gauche ;

– $H_1: z \neq 0$ , soit $|z| > z_{\frac{\alpha}{2}, 0, 1}$ , pour un test bilatéral.

La table de la loi normale centrée-réduite

Calcul de la p-valeur exacte si $n < 25$

– Calculer $m = n \cdot p$ , la proportion attendue au sein de l’effectif.

– Si $n_1 = m$ alors $p = 1$ .

– Sinon, on pose $s = \sharp \lbrace i \in I; \mathbb{P}_{n,p} (i) \leq b \rbrace$ et,

Si $n_1 < m$ alors calculer $s$ sur $I = [m,n]$ et la p-valeur de forme :

$p = \mathbb{P}_{B(n, p)} (X \leq n_1) + \mathbb{P}_{B(n, p)} (X > n - s)$

Si $n_1 > m$ alors calculer $s$ sur $I = [0,m]$ et la p-valeur de forme :

$p = \mathbb{P}_{B(n, p)} (X \leq s - 1) + \mathbb{P}_{B(n, p)} (X > n_1 - 1)$

On a défini là la version bilatéral du test. Pour passer sur une version unilatéral à droite il faut se contenter d’utiliser le terme de gauche, tandis que pour celle forme à gauche ce sera celui de droite.

Calcul de la p-valeur exacte si $n \geq 25$

La loi à laquelle reporter la statistique de test $z$ est celle de la loi normale centrée-réduite. Étant donné que sa fonction de répartition est basée sur la fonction erreur $erf(.)$ , il conviendra de passer par la méthode analytique proposée par Abramowitz et Stegun et permettant une estimation fiable à $10 ^{-7}$ prés. Soit le changement de variable suivant,

$t = \frac{1}{1 + 0.2316419 \cdot z}$

La formule d’usage et faisant intervenir aussi bien $z$ que sa transformée $t$ est,

$p = 1 - F_{L(0,1)} (Z) = 1 - \frac{1}{\sqrt{2 \pi}} e ^{-\frac{z ^2}{2}} \sum_{k = 1} ^5 t ^k C_k$

Avec,

– $C_1 = 0.319381530$ ;

– $C_2 = -0.356563782$ ;

– $C_3 = 1.781477937$ ;

– $C_4 = -1.821255978$ ;

– $C_5 = 1.330274429$ .

Tendance pour le rejet de $H_0$

En fonction de la taille d’échantillon, deux approches sont à considérer. Pour la plus simple ( $n \geq 25$ ), il est trivial de voir que plus la valeur observée $b$ s’éloigne de l’espérance plus on a de chance de rejeter $H_0$ .

Pour celle un peu plus complexe ( $n< 25$ ), soit $n_1 = m$ et donc la distribution est aléatoire ce qui implique le rejet de $H_0$ . Soit $n_1 \neq m$ et alors on rejette $H_0$ si,

– $\mathbb{P}_{B(n, p)} (X \leq n_1) + \mathbb{P}_{B(n, p)} (X > n - s) \rightarrow 0$

– $\mathbb{P}_{B(n,p)} (X \leq s - 1) + \mathbb{P}_{B(n, p)} (X > n_1 - 1) \rightarrow 0$

Puisqu’une probabilité ne peut pas être négative, finalement la méthode consiste à comparer directement la probabilité ce qui se passe sur les queues de la distribution. Plus elles sont lourdes et moins on a de chances de rejeter $H_0$ .

$\bullet$ Tendance lorsque $n \longrightarrow \infty$ :

On s’intéresse désormais à la résistance du test binomial au fur et à mesure que la taille d’échantillon croît. Etant donné que la statistique de test suit une loi normale centrée-réduite, elle-même indépendante de $N$ , on cherchera à étudier la résistance de la formule de $b$ directement. On travaille sur une répartition présentant pour chaque cellule les mêmes effectifs, que l’on multiplie selon la taille de l’échantillon et à laquelle on apporte une correction selon une loi uniforme dans $[0,1]$ , soit un cas fictif correspondant à l’indépendance entre $X ^1$ et $X ^2$ . Le résultat attendu sera donc que quelque soit la taille de l’échantillon, l’on ne devrait pas rejeter l’hypothèse $H_0$ d’inégalité des deux proportions. Le graphique ci-dessous montre l’évolution de la p-valeur $p$ associée au test binomial lorsque $n$ croît de $10$ à $100000$ observations.

De manière hâtive, on reste en adéquation avec l’hypothèse de construction de la statistique de test binomial jusqu’à $n \approx 20000$ ( $p > 20 \%$ ). En montant à $n \approx 50000$ , on se forcera à rejeter $H_0$ avec un risque assez fort compris entre $5 \%$ et $20 \%$ . Enfin, à $n \approx 80000$ la p-valeur passe en dessous des $1 \%$ .

Cette simulation montre que le test binomial est assez robuste à la malédiction des grands échantillons.

$\bullet$ Annexe théorique :

On présente ici la démonstration du calcul de l’espérance et de la variance de la loi Binomiale.

Dans un premier temps, il faut savoir que si $X$ suit une loi Binomiale de paramètres $(n,p)$ alors la variable aléatoire peut être considérée comme la somme de $n$ variables aléatoires $X_i$ indépendantes et suivant une loi de Bernoulli de paramètre $p$ . Cette dernière se caractérise par les éléments suivants,

$\mathbb{E}[X_i] = p$ et $V(X_i) = p (1 - p)$

Dès lors, on a,

$\mathbb{E}[X] = \mathbb{E}[\sum_{i = 1} ^n X_i] = \sum_{i = 1} ^n \mathbb{E}[X_i] = \sum_{i = 1} ^n p = n \cdot p$

Et,

$V(X) = V(\sum_{i = 1} ^n X_i) = \sum_{i = 1} ^n V(X_i) = \sum_{i = 1} ^n p \cdot q = n \cdot p \cdot q$

$\bullet$ Exemple :

Soit l’échantillon suivant,

$\begin{tabular}{|c|} \hline X \\ \hline A \\ \hline A \\ \hline A \\ \hline B \\ \hline B \\ \hline B \\ \hline B \\ \hline A \\ \hline A \\ \hline A \\ \hline A \\ \hline B \\ \hline B \\ \hline B \\ \hline B \\ \hline B \\ \hline B \\ \hline B \\ \hline B \\ \hline B \\ \hline \end{tabular}$

Afin d’illustrer cet exemple, on réalise un diagramme en camembert :

On a $n_1 = \sharp \lbrace X = "A" \rbrace = 7$ et $\sharp \lbrace X = "B" \rbrace = 13$ . Il semblerait donc que $X$ ne soit pas distribuée équitablement. On fixe alors $p = \frac{1}{2}$ .

Donc,

$b = \mathbb{P}_{20,\frac{1}{2}} (7)$

$= \binom{20}{7} \cdot \frac{1}{2} ^7 \cdot (1 - \frac{1}{2}) ^{20 - 7}$

$= \frac{20!}{7! \times (20 - 7)!} \times 0.078125 \times 0.0001220703$

$= 77520 \times 0.0000009536743$

$=0.07392883$

Maintenant que l’on a la statistique de test, on souhaite déterminer la p-valeur. Comme $n = 20 < 25$ alors on utilise l’approche par méthode de Monte-Carlo :

$m = 20 \times 0.5 = 10$

Or $n_1 < m$ , donc on travaillera sur l’intervalle $[10,20]$ . On a $\forall i \in[10,20]$ ,

$\mathbb{P}_{20,\frac{1}{2}} (i) = (0.17619705,0.16017914,0.12013435,0.07392883$

$,0.03696442,0.01478577,0.004620552,0.001087189$

$,0.0001811981,0.00001907349)$

D’où,

$s = \sharp \lbrace i \in [10;20]; \mathbb{P}_{20,\frac{1}{2}} (i) \leq 0.07392883 \rbrace = 7$

Enfin,

$p = P_{B(20,\frac{1}{2})} (X \leq 7) + P_{B(20,\frac{1}{2})} (X > 20 - 7)$

$= P_{B(20,\frac{1}{2})} (X \leq 7) + P_{B(20,\frac{1}{2})} (X > 13)$

$= \sum_{k = 1} ^7 P_{B(20,\frac{1}{2})} (X = k) + (1 - \sum_{ k = 1} ^{12} P_{B(20,\frac{1}{2})} (X = k))$

$= 0.131588 + (1 - 0.8684111)$

$= 0.131587 + 0.1315889$

$= 0.2631759 > 5 \%$

On en conclut que l’on ne peut pas rejeter $H_0$ et donc que les deux modalités ne sont pas distribuées selon la répartition de référence.

$\bullet$ Application sous R :

Soit l’exemple suivant :

X = c(« A », »A », »A », »B », »B », »B », »B », »A », »A », »A », »A », »B », »B », »B », »B », »B », »B », »B », »B », »B »)

Package et fonction R : https://stat.ethz.ch/R-manual/R-devel/library/stats/html/binom.test.html

La fonction binom.test du package stats permet de lancer le test binomial afin de comparer la répartition des modalités de $X$ à la référence : $\frac{1}{2}$ . On procède de la manière suivante :

binom.test(x = table(X), p = 0.5, alternative = « two.sided »)

Parmi les éléments à insérer les plus importants il faut relever :

– La variable que l’on souhaite étudier : $x = table(X)$ ;

– La proportion de référence : $p = 0.5$ ;

– La version bilatérale du test : $alternative = "two.sided"$ .

On obtient les résultats suivants :

On vérifie :

– La proportion observée : « number of successes $= 7$ » ;

– La taille de l’échantillon : « number of trials $= 20$ » ;

– La p-valeur : « $p-value = 20$ » , qui est la même que celle obtenue lors des calculs manuels (cf section « Exemple »).

$\bullet$ Application sous SAS :

Soit l’exemple suivant :

data E;
input X $1.;
cards;
A
A
A
B
B
B
B
A
A
A
A
B
B
B
B
B
B
B
B
B
;
run;

Procédure SAS: http://support.sas.com/documentation/cdl/en/procstat/63104/HTML/default/procstat_freq_sect028.htm

La procédure FREQ permet de lancer le test binomial afin de comparer la répartition des modalités de $X$ à la référence : $\frac{1}{2}$ . On procède de la manière suivante :

proc freq data = E;
tables X / binomial (equiv p = 0.5);
run;

Parmi les éléments à insérer les plus importants il faut relever :

– La variable que l’on souhaite croiser : tables X ;

– L’utilisation du test binomial : $/ binomial$ ;

– La proportion de référence : $(equip$ $p = 0.5)$ .

On obtient les résultats suivants :

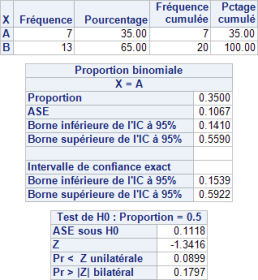
On vérifie :

– Le premier tableau qui donne les effectifs par modalité de $X$ ;

– Dans le second tableau, on retrouve des éléments descriptifs dont la proportion observée ainsi que les intervalles de confiance ;

– Dans le troisième tableau, on retrouve la p-valeur $Pr > |Z|$ bilatéral $= 0.1797$ qui diffère de celle obtenue lors des calculs manuels (cf section « Exemple ») du fait que SAS utilise quelque soit la taille de l’échantillon le z-score et la loi normale centrée-réduite, aboutissant cependant aux mêmes conclusions.

$\bullet$ Bibliographie :

– Statistique. Dictionnaire encyclopédique de Yadolah Dodge ;

– The use of confidence or fiducial limits illustrated in the case of the binomial de C. J. Clopper et E. S. Pearson ;

– Goodness-of-fit statistics for discrete multivariate data de T. R. C. Read et N. A. C. Cressie.

lemakistatheux

Youhou Mayotte c'est la fête…

Le test binomial

Laisser un commentaire Annuler la réponse.

Partager :

Laisser un commentaire Annuler la réponse.